Você está aqui: Java ::: Dicas & Truques ::: Métodos Numéricos - Programação Numérica

Como calcular integral em Java usando a Regra dos Trapézios - Java para Métodos Numéricos

Quantidade de visualizações: 112 vezes

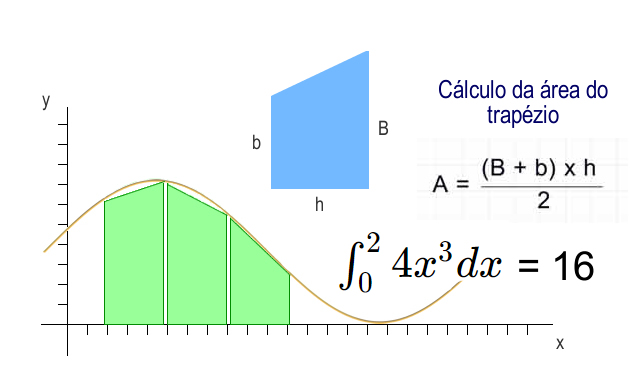A regra dos trapézios é um método de aproximação da integral definida de uma função. Baseia-se na ideia de aproximar a área sob uma curva por uma série de trapézios em vez de retângulos, dando uma estimativa mais precisa.

Veja o código Java completo para uma aplicação na qual usamos a soma das áreas dos trapézios representando a área abaixo de uma função e retornamos a integral dessa função para diferentes quantidades de trapézios:

Este trecho de código ou resolução de exercício faz parte do Super Pack 12.000 Dicas e Truques de Programação e 1.500 Exercícios Resolvidos em Java, Python, VisuAlg, Portugol, Delphi, C#, C, C++, VB.NET, Golang, Pascal, Ruby, PHP, e várias outras linguagens.

Aprenda a programar resolvendo problemas do mundo real. Tudo em português, com comentários em português.

Quero Ser Apoiador(a)

Ao executar este código Java nós teremos o seguinte resultado:

Valor da integral com 5 trapézios: 17.0
Valor da integral com 10 trapézios: 16.197530864197525
Valor da integral com 50 trapézios: 16.006663890045807
Valor da integral com 100 trapézios: 16.001632486480972
Valor da integral com 1000 trapézios: 16.000016032048062

Por este resultado fica claro que, quanto maior o número de trapézios dividindo a área abaixo da função, maior é a precisão do cálculo.

Link para compartilhar na Internet ou com seus amigos:

Desafios, Exercícios e Algoritmos Resolvidos de Java

Escreva um programa Java para exibir a soma dos cubos de dois números informados pelo usuário. Faça a leitura da entrada do usuário - Exercícios Resolvidos de Java

Como converter quilômetros em metros, centímetros e milímetros usando Java - Exercício Resolvido de Java

Escreva um programa Java que pede para o usuário informar o salário de uma pessoa, o valor de um empréstimo e a quantidade de prestações - Exercício Resolvido de Java

Algorítmos Resolvidos de Java - A classe Retangulo (construtores, getters e setters, encapsulamento e static) - Exercício Resolvido de Java

Como calcular o comprimento de um segmento de reta usando Java - Exercícios Resolvidos de Java

Receber um nome e imprimir as 4 primeiras letras do nome - Exercício Resolvido de Java

Como testar se um ano é bissexto em Java - Um programa que lê um ano com quatro dígitos e informa se ele é bissexto ou não - Exercícios Resolvidos de Java

Um programa que solicita ao usuário que informe um número e verifica se tal número é um número perfeito - Exercícios Resolvidos de Java

Escreva um programa Java que inverte uma palavra, frase ou texto usando recursividade - Exercício Resolvido de Java

Declarar e construir um vetor, pedir ao usuário para informar os valores dos elementos e mostrar o maior e o menor valor armazenado no vetor - Exercícios Resolvidos de Java

Valor da diária, valor médio arrecadado com e sem promoção e o lucro ou prejuízo mensal de uma promoção em um hotel - Exercício Resolvido de Java

Como resolver o problema da Subsequência de Soma Máxima em Java usando o Algorítmo de Kadane - Exercícios Resolvidos de Java

Escreva um programa Java para remover e retornar o terceiro elemento de uma ArrayList - Exercícios Resolvidos de Java

Como testar se um número é positivo ou negativo em Java - Exercício Resolvido de Java

Como remover um nó no início de uma lista duplamente encadeada em Java - Escreva um programa Java que cria uma lista - Exercício Resolvido de Java

Listando arquivos e diretórios em um diretório informado pelo usuário - Exercícios Resolvidos de Java

Exercícios Resolvidos de Física usando Java - (Unitau) Uma motocicleta com velocidade constante de 20 m/s ultrapassa um trem de comprimento 100 m e velocidade 15 m/s. A duração da ultrapassagem... - Exercício Resolvido de Java

A loja ELETROMÓVEIS está vendendo os seus produtos no cartão em 5 vezes sem juros. Faça um algoritmo Java que - Exercícios Resolvidos de Java

Um programa Java console ou GUI que receberá a duração de um evento expresso em segundos e exiba-o expresso em horas, minutos e segundos - Exercício Resolvido de Java

Como transformar dias em anos, meses, semanas e dias em Java - Exercícios Resolvidos de Java

Como criar uma matriz bidimensional em Java - Escreva um programa Java que declara uma matriz de duas dimensões e pede - Exercício Resolvido de Java

Um método recursivo que calcula o fatorial de um determinado número inteiro - Exercícios Resolvidos de Java

O desafio do triângulo alinhado à direita - Exercício Resolvido de Java

Escreva um programa Java que pede para o usuário informar o seu nome e seu sobrenome, cada um em variáveis separadas. Faça a validação - Exercício Resolvido de Java

Como montar uma string contendo o primeiro caractere, o caractere do meio e o último caractere de uma string informada - Exercícios Resolvidos de Java

Quantidade de patas dos animais de uma fazenda - O desafio da fazenda em Java - Exercícios Resolvidos de Java

Internet, Rede e E-Mail - Exercício Resolvido 1 - Exercícios Resolvidos de Java

Como encontrar o maior valor em um ArrayList de inteiros usando Collections.max() - Exercícios Resolvidos de Java

Como testar se uma matriz é uma Matriz Triangular Superior em Java - Exercícios Resolvidos de Java

Um programa Java que lê dois números e mostra a soma, subtração, multiplicação e a divisão dos números lidos - Exercícios Resolvidos de Java

Veja mais Dicas e truques de Java

Como excluir uma tabela MySQL usando a instrução DROP TABLE e o método executeUpdate() da classe Statement do Java

Exercícios Resolvidos de Java - Escreva um programa Java que inverte uma palavra, frase ou texto usando recursividade

Como encontrar valores duplicados em um array em Java usando as Streams do Java 8

Como pesquisar uma substring em uma string usando método matches da classe String e expressões regulares

Exercício Resolvido de Java - Fazer um programa para receber um número inteiro de segundos do usuário e imprimir a quantidade correspondente em horas

Como usar o método yield() para parar a thread atual e ceder a CPU para outras threads

Como efetuar captura de tela (screenshot) em seus programas Java usando o método createScreenCapture() da classe Robot

Java Swing - Como colorir as células de uma JTable individualmente ao passar o mouse sobre elas

Exercícios Resolvidos de Java - Uma loja está concedendo desconto de 20% para clientes do sexo feminino com idade entre 18 e 35 anos (ambas incluídas)

Como gerar 10 números randômicos sem repetição em Java usando as classes Random e LinkedHashSet

Dicas e truques de outras linguagens

Java - Como ligar ou desligar a tecla Caps Lock do seu teclado usando Java

C# - Como calcular raiz quadrada em C# usando a função Sqrt() da classe Math

Delphi - Como escrever uma função recursiva para calcular a potência de um número em Delphi

JavaScript - Como calcular juros simples e montante usando JavaScript

Java - Java Swing - Como criar sua primeira JTree usando um vetor de nomes de linguagens de programação

Revit C# - Como criar um formulário Windows Forms a partir do Revit C#

Excel - Como gerar números aleatórios inteiros entre 1 e 10 no Excel usando as funções ALEATÓRIO() e INT()

C - Como escrever uma função concat() que reproduz a funcionalidade da função strcat() da linguagem C

Java - Como verificar se Num Lock está ativado no seu teclado usando o método getLockingKeyState() da classe Toolkit da linguagem Java

Delphi - Como usar a propriedade Items da classe TComboBox do Delphi

E-Books em PDF

E-Book 350 Exercícios Resolvidos de Java - PDF com 500 páginas

Domine lógica de programação e a linguagem Java com o nosso E-Book 350 Exercícios Exercícios de Java, para você estudar onde e quando quiser.

Este e-book contém exercícios resolvidos abrangendo os tópicos: Java básico, matemática e estatística, programação dinâmica, strings e caracteres, entrada e saída, estruturas condicionais, vetores e matrizes, funções, laços, recursividade, internet, arquivos e diretórios, programação orientada a objetos e muito mais.

Ver Conteúdo do E-book

E-Book 650 Dicas, Truques e Exercícios Resolvidos de Python - PDF com 1.200 páginas

Domine lógica de programação e a linguagem Python com o nosso E-Book 650 Dicas, Truques e Exercícios Exercícios de Python, para você estudar onde e quando quiser.

Este e-book contém dicas, truques e exercícios resolvidos abrangendo os tópicos: Python básico, matemática e estatística, banco de dados, programação dinâmica, strings e caracteres, entrada e saída, estruturas condicionais, vetores e matrizes, funções, laços, recursividade, internet, arquivos e diretórios, programação orientada a objetos e muito mais.

Ver Conteúdo do E-book

Linguagens Mais Populares

1º lugar: Java
2º lugar: Python
3º lugar: C#
4º lugar: PHP
5º lugar: C
6º lugar: Delphi
7º lugar: JavaScript
8º lugar: C++
9º lugar: VB.NET
10º lugar: Ruby

Você está aqui: Java ::: Dicas & Truques ::: Métodos Numéricos - Programação Numérica

Como calcular integral em Java usando a Regra dos Trapézios - Java para Métodos Numéricos

Questões de Concurso para Engenharia Civil

Exercícios Resolvidos

Bancos de Dados

Questões de Concurso

Frameworks

Projetos e Códigos Fonte

Especializações

Calculadoras

Ferramentas

Todas as Linguagens, Frameworks, Biliotecas e Bancos de Dados

Compre pelo WhatsApp: +55 (062) 98553-6711

E-Book 650 Dicas, Truques e Exercícios Resolvidos de Python - Com comentários em Português

PDF COM 1.200 PÁGINAS

Apenas R$ 32,90