Você está aqui: C++ ::: Desafios e Lista de Exercícios Resolvidos ::: Engenharia Civil - Cálculo Estrutural |
|
Como calcular as reações de apoio, momento de flexão máxima e forças cortantes em uma viga bi-apoiada com carga distribuída retangular usando C++ - Desafio de Programação Resolvido em C++Quantidade de visualizações: 1141 vezes |
|
|
Pergunta/Tarefa: Veja a seguinte figura: 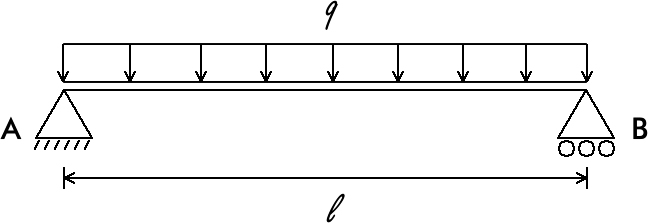 Nesta imagem temos uma viga bi apoiada com uma carga q distribuída de forma retangular a uma distância l. Para fins didáticos, vamos considerar que a carga q será em kN/m e a distância l será em metros. O apoio A é de segundo gênero e o apoio B é de primeiro gênero. Escreva um programa C++ que solicita ao usuário que informe o valor da carga q e a distância l entre os apoios A e B. Em seguida mostre os valores das reações nos apoios A e B, o momento de flexão máxima da viga e o momento de flexão para uma determinada distância (que o usuário informará) a partir do apoio A. Mostre também as forças cortantes nos apoios A e B. Lembre-se de que, para uma carga distribuída de forma retangular, o diagrama de momento fletor é uma parábola, enquanto o diagrama de cortante é uma reta (com o valor zero para a força cortante no meio da viga). Sua saída deve ser parecida com: Valor da carga em kN/m: 10 Distância em metros: 13 A reação no apoio A é: 65.000000 kN A reação no apoio B é: 65.000000 kN O momento fletor máximo é: 211.250000 kN Informe uma distância a partir do apoio A: 4 O momento fletor na distância informada é: 180.000000 kN A força cortante no apoio A é: 65.000000 kN A força cortante no apoio B é: -65.000000 kN Veja a resolução comentada deste exercício usando C++:
|
|
|
|
|
Mais Desafios de Programação e Exercícios e Algoritmos Resolvidos de C++ |
Veja mais Dicas e truques de C++ |
Dicas e truques de outras linguagens |
|
PHP - PHP para iniciantes - Como obter a diferença em horas entre duas datas (e suas respectivas horas) |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |






