 |
|
Você está aqui: Portugol ::: Portugol para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como somar os elementos da diagonal principal de uma matriz em PortugolQuantidade de visualizações: 350 vezes |
|
A Matriz quadrada é um tipo especial de matriz que possui o mesmo número de linhas e o mesmo número de colunas, ou seja, dada uma matriz Anxm, ela será uma matriz quadrada se, e somente se, n = m, onde n é o número de linhas e m é o número de colunas. Em geral as matrizes quadradas são chamadas de Matrizes de Ordem n, onde n é o número de linhas e colunas. Dessa forma, uma matriz de ordem 4 é uma matriz que possui 4 linhas e quatro colunas. Toda matriz quadrada possui duas diagonais, e elas são muito exploradas tanto na matemática quanto na construção de algorítmos. Essas duas diagonais são chamadas de Diagonal Principal e Diagonal Secundária. A diagonal principal de uma matriz quadrada une o seu canto superior esquerdo ao canto inferior direito. Veja: 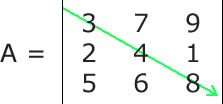 Nesta dica veremos como calcular a soma dos valores dos elementos da diagonal principal de uma matriz usando Portugol. Para isso, só precisamos manter em mente que a diagonal principal de uma matriz A é a coleção das entradas Aij em que i é igual a j. Assim, tudo que temos a fazer é converter essa regra para código Portugol. Veja um trecho de código Portugol completo no qual pedimos para o usuário informar os elementos da matriz e em seguida mostramos a soma dos elementos da diagonal superior: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
// Somar os elementos da diagonal principal de uma matriz
programa {
funcao inicio() {
// vamos declarar e construir uma matriz de três linhas
// e três colunas
inteiro matriz[3][3]
// guarda a soma dos elementos na diagonal principal
inteiro soma_diagonal = 0
// vamos pedir para o usuário informar os valores
// dos elementos da matriz, uma linha de cada vez
para (inteiro i = 0; i < 3; i++) {
para (inteiro j = 0; j < 3; j++) {
escreva("Informe o valor para a linha ", i, " e coluna ", j, ": ")
leia(matriz[i][j])
}
}
// vamos mostrar a matriz da forma que ela foi informada
escreva("\nValores na matriz:\n\n")
para (inteiro i = 0; i < 3; i++) {
para (inteiro j = 0; j < 3; j++) {
escreva(matriz[i][j], " ")
}
// passa para a próxima linha da matriz
escreva("\n")
}
// vamos calcular a soma dos elementos da diagonal
// principal
para (inteiro i = 0; i < 3; i++) {
para (inteiro j = 0; j < 3; j++) {
se (i == j) {
soma_diagonal = soma_diagonal + matriz[i][j]
}
}
}
// finalmente mostramos a soma da diagonal principal
escreva("\nA soma dos elementos da diagonal principal é: ", soma_diagonal)
}
}
Ao executar este código Portugol nós teremos o seguinte resultado: Informe o valor para a linha 0 e coluna 0: 3 Informe o valor para a linha 0 e coluna 1: 7 Informe o valor para a linha 0 e coluna 2: 9 Informe o valor para a linha 1 e coluna 0: 2 Informe o valor para a linha 1 e coluna 1: 4 Informe o valor para a linha 1 e coluna 2: 1 Informe o valor para a linha 2 e coluna 0: 5 Informe o valor para a linha 2 e coluna 1: 6 Informe o valor para a linha 2 e coluna 2: 8 3 7 9 2 4 1 5 6 8 A soma dos elementos da diagonal principal é: 15 |
 Link para compartilhar na Internet ou com seus amigos: |
Portugol ::: Dicas & Truques ::: Matemática e Estatística |
Como resolver uma equação do segundo grau em Portugol - Como calcular Bhaskara em PortugolQuantidade de visualizações: 2313 vezes |
|
Como resolver uma equação do 2º grau usando Portugol Nesta dica mostrarei como encontrar as raízes de uma equação quadrática, ou seja, uma equação do 2º usando um algoritmo escrito na ferramenta Portugol Studio, uma das preferidas para o aprendizado de algoritmos e lógica de programação. Definimos como equação do 2º grau ou equações quadráticas qualquer equação do tipo ax² + bx + c = 0 em que a, b e c são números reais e a ≠ 0. Ela recebe esse nome porque, no primeiro membro da igualdade, há um polinômio de grau dois com uma única incógnita. Note que, dos coeficientes a, b e c, somente o a é diferente de zero, pois, caso ele fosse igual a zero, o termo ax² seria igual a zero, logo a equação se tornaria uma equação do primeiro grau: bx + c = 0. Independentemente da ordem da equação, o coeficiente a sempre acompanha o termo x², o coeficiente b sempre acompanha o termo x, e o coeficiente c é sempre o termo independente. Como resolver uma equação do 2º grau Conhecemos como soluções ou raízes da equação ax² + bx + c = 0 os valores de x que fazem com que essa equação seja verdadeira. Uma equação do 2º grau pode ter no máximo dois números reais que sejam raízes dela. Para resolver equações do 2º grau completas, existem dois métodos mais comuns: a) Fórmula de Bhaskara; b) Soma e produto. O primeiro método é bastante mecânico, o que faz com que muitos o prefiram. Já para utilizar o segundo, é necessário o conhecimento de múltiplos e divisores. Além disso, quando as soluções da equação são números quebrados, soma e produto não é uma alternativa boa. Como resolver uma equação do 2º grau usando Bhaskara Como nosso algoritmo Portugol vai resolver a equação quadrática usando a Fórmula de Bhaskara, o primeiro passo é encontrar o determinante. Veja: \[\Delta =b^2-4ac\] Nem sempre a equação possui solução real. O valor do determinante é que nos indica isso, existindo três possibilidades: a) Se determinante > 0, então a equação possui duas soluções reais. b) Se determinante = 0, então a equação possui uma única solução real. c) Se determinante < 0, então a equação não possui solução real. Encontrado o determinante, só precisamos substituir os valores, incluindo o determinante, na Fórmula de Bhaskara: \[x = \dfrac{- b\pm\sqrt{b^2- 4ac}}{2a}\] Vamos agora ao código Portugol (escrevi e testei no Portugol Webstudio). Nossa aplicação vai pedir para o usuário informar os valores dos três coeficientes a, b e c e, em seguida, vai apresentar as raizes da equação: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
// "Como resolver uma equação do 2º grau usando Portugol
programa {
// inclui a biblioteca Matematica
inclua biblioteca Matematica --> mat
// função principal do programa
funcao inicio() {
// variáveis usadas na resolução do problema
// os coeficientes
real a, b, c
// as duas raizes, a imaginaria e o discriminante
real raiz1, raiz2, imaginaria, discriminante
// vamos pedir para o usuário informar os valores dos coeficientes
escreva("Valor do coeficiente a: ")
leia(a)
escreva("Valor do coeficiente b: ")
leia(b)
escreva("Valor do coeficiente c: ")
leia(c)
// vamos calcular o discriminante
discriminante = (b * b) - (4 * a * c)
// a equação possui duas soluções reais?
se (discriminante > 0) {
raiz1 = ((b * -1) + mat.raiz(discriminante, 2.0)) / (2 * a)
raiz2 = ((b * -1) - mat.raiz(discriminante, 2.0)) / (2 * a)
escreva("Duas raizes: x1 = ", raiz1, " e x2 = ", raiz2)
}
// a equação possui uma única solução real?
senao se (discriminante == 0){
raiz1 = (b * -1) / (2 * a)
raiz2 = (b * -1) / (2 * a)
escreva("Duas raizes iguais: x1 = ", raiz1, " e x2 = ", raiz2)
}
// a equação não possui solução real?
senao{
raiz1 = (b * -1) / (2 * a)
raiz2 = (b * -1) / (2 * a)
imaginaria = mat.raiz((discriminante * -1), 2.0) / (2 * a)
escreva("Existem duas raízes complexas: ")
escreva("x1 = ", raiz1, " + " ,imaginaria, " e x2 = ", raiz2, " - ", imaginaria)
}
}
}
Ao executar este código Portugol nós teremos o seguinte resultado: Valor do coeficiente a: 1 Valor do coeficiente b: 2 Valor do coeficiente c: -3 Existem duas raizes: x1 = 1.0 e x2 = -3.0 |
Portugol ::: Dicas & Truques ::: Cadeias e Caracteres |
Como testar se uma sub-cadeia está contida em uma cadeia de caracteres em Portugol usando a função posicao_texto()Quantidade de visualizações: 280 vezes |
|
Nesta dica mostrarei como podemos verificar se uma substring está contida em uma string em Portugol. Para isso nós vamos usar a função posicao_texto() da biblioteca Texto. A função posicao_texto() pede a sub-cadeia a ser pesquisada, a cadeia na qual a pesquisa será feita e o índice do primeiro caractere a partir do qual a sub-string será pesquisada. Se a substring for encontrada, a função retorna a posição do primeiro caractere. Caso contrário o valor -1 será retornado. Veja o código completo para um programa Portugol no qual testamos se uma palavra está contida em uma frase: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
programa {
// vamos importar a biblioteca Texto
inclua biblioteca Texto --> tx
funcao inicio() {
// vamos criar uma frase
cadeia frase = "Gosto de programar em Portugol"
// vamos criar uma sub-cadeia
cadeia palavra = "Portugol"
// vamos verificar se a sub-cadeia está contida na cadeia
se (tx.posicao_texto(palavra, frase, 0) != -1) {
escreva("A substring está contida na string")
}
senao {
escreva("A substring não está contida na string")
}
}
}
Ao executar este código Portugol nós teremos o seguinte resultado: A substring está contida na string. |
Portugol ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em Portugol dados dois pontos no plano cartesianoQuantidade de visualizações: 461 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem Portugol que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
// Calcular o coeficiente angular de uma reta em Portugol
programa {
// vamos incluir a biblioteca Matematica
inclua biblioteca Matematica --> mat
funcao inicio() {
// coordenadas dos dois pontos
real x1, y1, x2, y2
// guarda o coeficiente angular
real m
// x e y do primeiro ponto
escreva("Coordenada x do primeiro ponto: ")
leia(x1)
escreva("Coordenada y do primeiro ponto: ")
leia(y1)
// x e y do segundo ponto
escreva("Coordenada x do segundo ponto: ")
leia(x2)
escreva("Coordenada y do segundo ponto: ")
leia(y2)
// vamos calcular o coeficiente angular
m = (y2 - y1) / (x2 - x1)
// mostramos o resultado
escreva("O coeficiente angular é: ", m)
}
}
Ao executar este código Portugol Webstudio nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 3 Coordenada y do primeiro ponto: 6 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 10 O coeficiente angular é: 0.6666666666666666 No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
Desafios, Exercícios e Algoritmos Resolvidos de Portugol |
Veja mais Dicas e truques de Portugol |
Dicas e truques de outras linguagens |
Códigos Fonte |
 Software de Gestão Financeira com código fonte em PHP, MySQL, Bootstrap, jQuery - Inclui cadastro de clientes, fornecedores e ticket de atendimentoDiga adeus às planilhas do Excel e tenha 100% de controle sobre suas contas a pagar e a receber, gestão de receitas e despesas, cadastro de clientes e fornecedores com fotos e histórico de atendimentos. Código fonte completo e funcional, com instruções para instalação e configuração do banco de dados MySQL. Fácil de modificar e adicionar novas funcionalidades. Clique aqui e saiba mais |
 Controle de Estoque completo com código fonte em PHP, MySQL, Bootstrap, jQuery - 100% funcional e fácil de modificar e implementar novas funcionalidadesTenha o seu próprio sistema de controle de estoque web. com cadastro de produtos, categorias, fornecedores, entradas e saídas de produtos, com relatórios por data, margem de lucro e muito mais. Código simples e fácil de modificar. Acompanha instruções para instalação e criação do banco de dados MySQL. Clique aqui e saiba mais |
Linguagens Mais Populares |
|
1º lugar: Java |
