 |
|
|
|
Você está aqui: Portugol ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular a área do trapézio em Portugol - Portugol para Geometria PlanaQuantidade de visualizações: 2311 vezes |
Antes de passarmos ao código Portugol para o cálculo da área de um trapézio, dê uma olhada na imagem a seguir: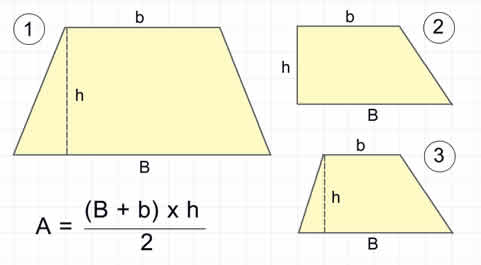 A área do trapézio é a medida correspondente a superfície dessa figura da geometria plana. O cálculo da sua área é o produto entre a soma das medidas das bases (B e b) pela altura (h), e dividindo o resultado por 2. O trapézio possui quatro lados, por isso ele é também um quadrilátero. Dois lados são as bases, e as bases são paralelas entre si. A base de maior medida é chamada de base maior (B), e a base de menor medida é chamada de base menor (b). Quais são os tipos de trapézio Podemos classificar os trapézios de acordo com suas formas e disposição no plano (e marcados na figura acima): 1) Trapézio Isósceles: possui dois lados com as mesmas medidas. 2) Trapézio Retângulo: possui dois ângulos retos (90°). Além disso, o lado que possui os ângulos retos é perpendicular as bases. E é também a altura do trapézio. Fique atento a este tipo de trapézio, pois ele é usado no cálculo numérico (métodos numéricos) para aproximar a integral de uma função usando a regra dos trapézios. 3) Trapézio Escaleno: todos os lados com medidas diferentes. Como calcular a área do trapézio em Portugol Agora que já vimos os três tipos diferentes de trapézios e vimos também a fórmula para o cálculo de sua área (na imagem acima), podemos passar ao código Portugol que pede para o usuário informar a medida da base maior, da base menor e da altura do trapézio e retornamos a sua área. Veja o exercício: 1) Seja um trapézio medindo 3 cm de altura, base maior medindo 8 cm e base menor medindo 5 cm. Calcule a área do trapézio. Eis o código Portugol para a resolução: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
// Como calcular a área de um trapézio em Portugol
programa {
funcao inicio() {
// variáveis usadas na resolução do problema
real b_maior, b_menor, altura, area
// vamos ler a medida da base maior
escreva("Medida da base maior (B): ")
leia(b_maior)
// vamos ler a medida da base menor
escreva("Medida da base menor (b): ")
leia(b_menor)
// vamos ler a medida da altura
escreva("Medida da altura (h): ")
leia(altura)
// e agora calculamos a área do trapézio
area = ((b_maior + b_menor) * altura) / 2.0
// e mostramos o resultado
escreva("A área do trapézio é: ", area, " cm quadrados.")
}
}
Ao executarmos este código Portugol nós teremos o seguinte resultado: Medida da base maior (B): 8 Medida da base menor (b): 5 Medida da altura (h): 3 A área do trapézio é: 19.5 cm quadrados. Tenha em mente que a área será sempre em centímetros quadrados, metros quadrados, quilômetros quadrados, etc. |
 Link para compartilhar na Internet ou com seus amigos: |
Desafios, Exercícios e Algoritmos Resolvidos de Portugol |
Veja mais Dicas e truques de Portugol |
Dicas e truques de outras linguagens |
|
Java - Como calcular a velocidade de um corpo dado sua massa e sua energia cinética usando a linguagem Java |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |
