 |
|
Você está aqui: VB.NET ::: VB.NET para Engenharia ::: Física - Mecânica - Estática |
Como calcular o centroide ou centro de gravidade de um triângulo em VB.NETQuantidade de visualizações: 278 vezes |
|
O centro de gravidade, ou centroide (centro geométrico), é o ponto no qual a massa de um triângulo se equilibra. Para ajudar a visualizar isso, imagine uma figura triangular suspensa sobre a ponta de um lápis. A figura vai se equilibrar se a ponta do lápis for posicionada em seu centro de gravidade. Encontrar o centroide pode ser necessário em vários projetos e aplicações de engenharia, e pode ser encontrado usando geometria simples. Veja a seguinte figura: 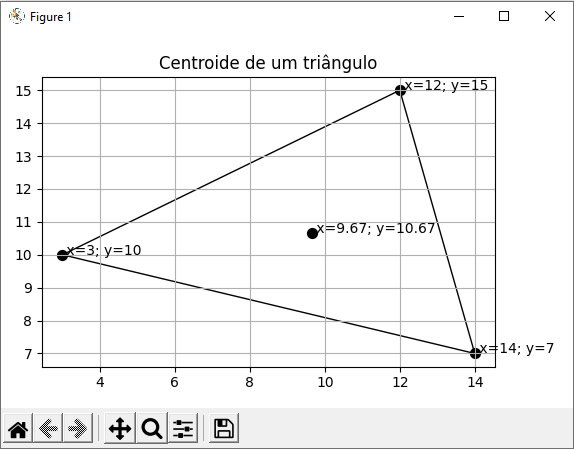 Nesta figura nós temos os três vértices do triângulo devidamente registrados, assim como o ponto representando seu centroide. Assim, a fórmula do centroide do triângulo é: \[x_c = \frac{x_1 + x_2 + x_3}{3}\] \[y_c = \frac{y_1 + y_2 + y_3}{3}\] Agora vamos ver como calcular o centro de gravidade do triângulo em VB.NET. Para isso nós vamos pedir para o usuário informar as coordenadas dos três vértices do triângulo e, em seguida, vamos mostrar as coordenadas do ponto que representa o centroide. Veja: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
Imports System
Module Program
' função principal do programa VB.NET
Sub Main(args As String())
' variáveis que usaremos na resolução do problema
Dim va_x, va_y, vb_x, vb_y, vc_x, vc_y, c_x, c_y As Double
' vamos ler as coordenadas do primeiro vértice
Console.Write("Informe o x do primeiro vértice: ")
va_x = Double.Parse(Console.ReadLine())
Console.Write("Informe o y do primeiro vértice: ")
va_y = Double.Parse(Console.ReadLine())
' vamos ler as coordenadas do segundo vértice
Console.Write("Informe o x do segundo vértice: ")
vb_x = Double.Parse(Console.ReadLine())
Console.Write("Informe o y do segundo vértice: ")
vb_y = Double.Parse(Console.ReadLine())
' vamos ler as coordenadas do terceiro vértice
Console.Write("Informe o x do terceiro vértice: ")
vc_x = Double.Parse(Console.ReadLine())
Console.Write("Informe o y do terceiro vértice: ")
vc_y = Double.Parse(Console.ReadLine())
' vamos calcular as coordenadas do centroide
c_x = (va_x + vb_x + vc_x) / 3.0
c_y = (va_y + vb_y + vc_y) / 3.0
' vamos mostrar o resultado
Console.WriteLine("As coordenadas do centroide são: x=" &
c_x & "; y=" & c_y)
Console.WriteLine(vbCrLf & "Pressione qualquer tecla para sair...")
' pausa o programa
Console.ReadKey()
End Sub
End Module
Ao executar este código VB.NET nós teremos o seguinte resultado: Informe o x do primeiro vértice: 3 Informe o y do primeiro vértice: 10 Informe o x do segundo vértice: 12 Informe o y do segundo vértice: 15 Informe o x do terceiro vértice: 14 Informe o y do terceiro vértice: 7 As coordenadas do centroide são: x=9.67; y=10.67 |
 Link para compartilhar na Internet ou com seus amigos: |
VB.NET ::: Dicas & Truques ::: Strings e Caracteres |
Como declarar e inicializar uma string em VB.NET usando o operador NewQuantidade de visualizações: 8379 vezes |
|
Nesta dica mostrarei como podemos usar o operador New para criar e inicializar um novo objeto da classe String em VB.NET. Veja o código completo para o exemplo: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
Imports System
Module Program
Sub Main(args As String())
' declara uma variável do tipo String
Dim frase As String
' inicializa a string usando New
frase = New String("Você já conhece o site Arquivo de Códigos?")
' vamos mostrar o resultado
Console.WriteLine("A frase é: " & frase)
Console.WriteLine(vbCrLf & "Pressione qualquer tecla para sair...")
' pausa o programa
Console.ReadKey()
End Sub
End Module
Ao executar este código VB.NET nós teremos o seguinte resultado: A frase é: Você já conhece o site Arquivo de Códigos? |
VB.NET ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular a equação reduzida da reta em VB.NET dados dois pontos pertencentes à retaQuantidade de visualizações: 288 vezes |
|
Nesta dica de VB.NET veremos como calcular a equação reduzida da reta quando temos dois pontos pertencentes à esta reta. Não, nessa dica não vamos calcular a equação geral da reta, apenas a equação reduzida. Em outras dicas do site você encontra como como isso pode ser feito. Para relembrar: a equação reduzida da reta é y = mx + n, em que x e y são, respectivamente, a variável independente e a variável dependente; m é o coeficiente angular, e n é o coeficiente linear. Além disso, m e n são números reais. Com a equação reduzida da reta, é possível calcular quais são os pontos que pertencem a essa reta e quais não pertencem. Vamos começar então analisando a seguinte figura, na qual temos dois pontos que pertencem à uma reta:  Note que a reta da figura passa pelos pontos A(5, 5) e B(9, 2). Então, uma vez que já temos os dois pontos, já podemos calcular a equação reduzida da reta. Veja o código VB.NET completo para esta tarefa: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
Imports System
Module Program
' função principal do programa VB.NET
Sub Main(args As String())
' vamos ler as coordenadas do primeiro ponto
Console.Write("Coordenada x do primeiro ponto: ")
Dim x1 As Double = Double.Parse(Console.ReadLine())
Console.Write("Coordenada y do primeiro ponto: ")
Dim y1 As Double = Double.Parse(Console.ReadLine())
' vamos ler as coordenadas do segundo ponto
Console.Write("Coordenada x do segundo ponto: ")
Dim x2 As Double = Double.Parse(Console.ReadLine())
Console.Write("Coordenada y do segundo ponto: ")
Dim y2 As Double = Double.Parse(Console.ReadLine())
Dim sinal As String = "+"
' vamos calcular o coeficiente angular da reta
Dim m As Double = (y2 - y1) / (x2 - x1)
' vamos calcular o coeficiente linear
Dim n As Double = y1 - (m * x1)
' coeficiente linear menor que zero? O sinal será negativo
If n < 0 Then
sinal = "-"
n = n * -1
End If
' mostra a equação reduzida da reta
Console.WriteLine("Equação reduzida: y = " & m & "x" _
& " " & sinal & " " & n)
Console.WriteLine(vbCrLf & vbCrLf & "Pressione qualquer tecla para sair...")
' pausa o programa
Console.ReadKey()
End Sub
End Module
Ao executar este código VB.NET nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 5 Coordenada y do primeiro ponto: 5 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 2 Equação reduzida: y = -0,75x + 8,75 Para testarmos se nossa equação reduzida da reta está realmente correta, considere o valor 3 para o eixo x da imagem acima. Ao efetuarmos o cálculo: ---------------------------------------------------------------------- Se precisar de ajuda com o código abaixo, pode me chamar no WhatsApp +55 (62) 98553-6711 (Osmar) ---------------------------------------------------------------------- >> y = (-0.75 * 3) + 8.75 y = 6.5000 temos o valor 6.5 para o eixo y, o que faz com que o novo ponto caia exatamente em cima da reta considerada na imagem. |
VB.NET ::: Dicas & Truques ::: Strings e Caracteres |
Como contar as ocorrências de um caractere em uma string em VB.NET usando o método IndexOf()Quantidade de visualizações: 12626 vezes |
|
Nesta dica mostrarei como podemos usar o método IndexOf() da classe String do VB.NET e o laço While para contar quantas vezes um determinado caractere ocorre em uma palavra, frase ou string. Veja o código completo para o exemplo: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
Imports System
Module Program
Sub Main(args As String())
Dim frase As String = "Gosto muito de VB.NET e você?"
Dim letra As Char = "o"
Dim quant As Integer = 0
Dim pos As Integer = -1, pos_ant As Integer = -1
Dim cont As Integer = 0
' mostra a frase
Console.WriteLine("A frase é: " & frase)
While cont < frase.Length
pos = frase.IndexOf(letra, cont)
If pos <> pos_ant And pos <> -1 Then
Console.WriteLine("""" & letra &
""" encontrada na posição " & pos)
quant += 1
End If
cont += 1
pos_ant = pos
End While
' mostra a quantidade de ocorrências da letra "o"
Console.WriteLine("Encontrei " & quant & " ocorrências da " _
& "letra " & letra)
Console.WriteLine(vbCrLf & "Pressione qualquer tecla para sair...")
' pausa o programa
Console.ReadKey()
End Sub
End Module
Ao executar este código VB.NET nós teremos o seguinte resultado: A frase é: Gosto muito de VB.NET e você? "o" encontrada na posição 1 "o" encontrada na posição 4 "o" encontrada na posição 10 "o" encontrada na posição 25 Encontrei 4 ocorrências da letra o |
Vamos testar seus conhecimentos em Python |
| Qual das formas abaixo é válida para a criação de um DICIONÁRIO em Python? A) estados = ["SP": "SÃO PAULO", "GO": "GOIÁS"] B) estados = ("SP": "SÃO PAULO", "GO": "GOIÁS") C) estados = set("SP": "SÃO PAULO", "GO": "GOIÁS") D) estados = "SP": "SÃO PAULO", "GO": "GOIÁS" E) estados = {"SP": "SÃO PAULO", "GO": "GOIÁS"} Verificar Resposta Estudar Cards Todas as Questões |
Vamos testar seus conhecimentos em Fenômeno de Transportes e Hidráulica |
| Fórmula de Chézy Um canal reto e retangular tem 2,1m de largura e 1,2m de profundidade e está com uma declividade de fundo de 3°. Sendo o fator de atrito igual a 0,022, a vazão para escoamento uniforme será: A) 23,97m3/s. B) 25,78m3/s. C) 30,87m3/s. D) 37,00m3/s. E) 37,55m3/s. Verificar Resposta Estudar Cards Todas as Questões |
Vamos testar seus conhecimentos em JavaScript |
| Qual das formas abaixo é válida para a declaração e inicialização de variáveis em JavaScript? A) int a = 5; B) declare a = 5; C) var a = 5; D) def a = 5; E) variable a = 5; Verificar Resposta Estudar Cards Todas as Questões |
Vamos testar seus conhecimentos em Ética e Legislação Profissional |
| Responsabilidade civil no código de defesa do consumidor O fornecedor e o prestador de serviço estarão livres do dever de indenizar caso não haja dano reparável e ficar comprovado que: A) a culpa foi exclusiva do consumidor ou de terceiro. B) a culpa foi do fornecedor. C) ninguém teve culpa. D) todos tiveram culpa. E) não importa quem teve culpa. Verificar Resposta Estudar Cards Todas as Questões |
Vamos testar seus conhecimentos em |
| Características do concreto armado Os domínios de deformação em concreto armado são categorias que descrevem diferentes estados de deformação do material em relação às tensões aplicadas. Cada domínio corresponde a um comportamento específico do material e pode ser usado para entender como o concreto e o aço de reforço interagem sob diferentes condições de carga. Nesse sentido, assinale a alternativa que traz o domínio no qual as peças de concreto armado devem ser projetadas de modo a melhor aproveitar as resistências dos materiais. A) Domínio 1. B) Domínio 2. C) Domínio 3. D) Domínio 4. E) Domínio 5. Verificar Resposta Estudar Cards Todas as Questões |
Desafios, Exercícios e Algoritmos Resolvidos de VB.NET |
Veja mais Dicas e truques de VB.NET |
Dicas e truques de outras linguagens |
Códigos Fonte |
 Software de Gestão Financeira com código fonte em PHP, MySQL, Bootstrap, jQuery - Inclui cadastro de clientes, fornecedores e ticket de atendimentoDiga adeus às planilhas do Excel e tenha 100% de controle sobre suas contas a pagar e a receber, gestão de receitas e despesas, cadastro de clientes e fornecedores com fotos e histórico de atendimentos. Código fonte completo e funcional, com instruções para instalação e configuração do banco de dados MySQL. Fácil de modificar e adicionar novas funcionalidades. Clique aqui e saiba mais |
 Controle de Estoque completo com código fonte em PHP, MySQL, Bootstrap, jQuery - 100% funcional e fácil de modificar e implementar novas funcionalidadesTenha o seu próprio sistema de controle de estoque web. com cadastro de produtos, categorias, fornecedores, entradas e saídas de produtos, com relatórios por data, margem de lucro e muito mais. Código simples e fácil de modificar. Acompanha instruções para instalação e criação do banco de dados MySQL. Clique aqui e saiba mais |
Linguagens Mais Populares |
|
1º lugar: Java |
