Você está aqui: Java ::: Desafios e Lista de Exercícios Resolvidos ::: Arrays e Matrix (Vetores e Matrizes) |
Como testar se uma matriz é uma Matriz Triangular Superior em Java - Exercícios Resolvidos de JavaQuantidade de visualizações: 388 vezes |
|
Pergunta/Tarefa: Uma Matriz Triangular Superior é a matriz na qual todos os termos que estão abaixo da diagonal principal são iguais a zero e os termos que estão acima da diagonal principal são números reais. Veja um exemplo de Matriz Triangular Superior na imagem abaixo: 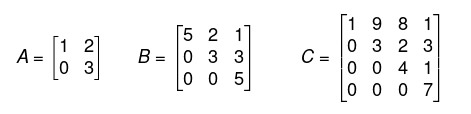 Escreva um programa Java que pede para o usuário informar o número de linhas e colunas de uma matriz quadrada. Em seguida solicite os valores para cada um dos elementos da matriz. Para finalizar informe ao usuário se a matriz informada é uma matriz triangular superior. Sua saída deverá ser parecida com:
Número de linhas e colunas da matriz: 3
Valor para a linha 0 e coluna 0: 8
Valor para a linha 0 e coluna 1: 2
Valor para a linha 0 e coluna 2: 3
Valor para a linha 1 e coluna 0: 0
Valor para a linha 1 e coluna 1: 3
Valor para a linha 1 e coluna 2: 9
Valor para a linha 2 e coluna 0: 0
Valor para a linha 2 e coluna 1: 0
Valor para a linha 2 e coluna 2: 2
Valores na matriz
8 2 3
0 3 9
0 0 2
A matriz é uma matriz triangular superior
Veja a resolução comentada deste exercício usando Java: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
package estudos;
import java.util.Scanner;
public class Estudos {
public static void main(String[] args) {
// para ler a entrada do usuário
Scanner entrada = new Scanner(System.in);
// vamos pedir a ordem da matriz
System.out.print("Número de linhas e colunas da matriz: ");
int ordem = Integer.parseInt(entrada.nextLine());
// agora vamos construir a matriz
int matriz[][] = new int[ordem][ordem];
// vamos ler os valores para os elementos da matriz
System.out.println();
for(int i = 0; i < ordem; i++){ // linhas
for(int j = 0; j < ordem; j++){ // colunas
System.out.print("Valor para a linha " + i + " e coluna " + j + ": ");
matriz[i][j] = Integer.parseInt(entrada.nextLine());
}
}
// vamos mostrar a matriz da forma que ela foi informada
System.out.println("\nValores na matriz\n");
for(int i = 0; i < ordem; i++){
for(int j = 0; j < ordem; j++){
System.out.printf("%5d ", matriz[i][j]);
}
// passa para a próxima linha da matriz
System.out.println();
}
// agora vamos testar se a matriz é uma matriz triangular
// superior
boolean triangular_superior = true;
for(int i = 0; i < ordem; i++){
for(int j = 0; j < ordem; j++){
// a condição para que a matriz seja triangular superior é
// que os elementos abaixo da diagonal principal sejam
// iguais a zero
if((j < i) && (matriz[i][j] != 0)){
triangular_superior = false;
}
}
}
if(triangular_superior){
System.out.println("\nA matriz é uma matriz triangular superior");
}
else{
System.out.println("\nA matriz não é uma matriz triangular superior");
}
}
}
Listamos abaixo algumas propriedades específicas da matriz triangular. 1) o determinante de uma matriz triangular é igual ao produto dos termos da diagonal principal. 2) o produto entre duas matrizes triangulares é uma matriz triangular. 3) se um dos termos da diagonal principal da matriz triangular for igual a zero, então o seu determinante será igual a zero e, consequentemente, ela não será inversível. 4) a matriz inversa de uma matriz triangular é também uma matriz triangular. 5) a soma de duas matrizes triangulares superiores é uma matriz triangular superior; de forma análoga, a soma de duas matrizes triangulares inferiores é uma matriz triangular inferior. |
|
|
Java ::: Dicas & Truques ::: Arquivos e Diretórios |
Como excluir um arquivo em Java usando o método delete() da classe File - Curso de Java para iniciantesQuantidade de visualizações: 14827 vezes |
|
Nesta dica mostrarei como podemos usar o método delete() da classe File da linguagem Java para excluir um arquivo no computador local. Se o arquivo for excluído com sucesso, o retorna será true, e false em caso contrário. Veja o código completo para o exemplo: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
package arquivodecodigos;
import java.io.*;
public class Estudos{
public static void main(String[] args){
File arquivo = new File("C:\\estudos_java\\osmar.txt");
if(arquivo.delete()){
System.out.println("Arquivo excluido com sucesso.");
}
else{
System.out.println("Não foi possivel excluir o arquivo");
}
}
}
Ao executar este código nós teremos o seguinte resultado: Arquivo excluido com sucesso. |
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Arrays e Matrix (Vetores e Matrizes) |
Exercícios Resolvidos de Java - Declarar e construir um vetor de inteiros e usar um laço for para inicializar seus elementos com os valores de 1 até 10 em JavaQuantidade de visualizações: 17268 vezes |
|
Pergunta/Tarefa: Escreva um programa Java que declara e constrói um array de 10 elementos do tipo int. Em seguida use um laço for para inicializar os elementos com os valores de 1 até 10. Para finalizar exiba os valores dos elementos do vetor na vertical. Seu programa deverá exibir a seguinte saída: 1 2 3 4 5 6 7 8 9 10 A resolução desta tarefa passa pela declaração e construção do array. Aqui eu demonstro como isso pode ser feito em dois passos. Primeiro a declaração e depois a construção: // vamos declarar um vetor de 10 ints int valores[]; // vamos construir o vetor...neste momento seus elementos // terão, todos, o valor 0 valores = new int[10]; Veja a resolução completa do exercício: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
public static void main(String[] args){
// vamos declarar um array de 10 ints
int valores[];
// vamos construir o array...neste momento seus elementos
// terão, todos, o valor 0
valores = new int[10];
// vamos usar o laço for para inicializar seus elementos
// com os valores de 1 até 10
for(int i = 0; i < valores.length; i++){
// aqui nós usamos o valor da variável i para acessar o
// elemento do array e também para atribuir o valor de i + 1
// ao elemento sendo acessado
valores[i] = (i + 1);
}
// só nos resta exibir os valores de todos os elementos
for(int i = 0; i < valores.length; i++){
System.out.println(valores[i]);
}
}
|
Java ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular a equação reduzida da reta em Java dados dois pontos pertencentes à retaQuantidade de visualizações: 1197 vezes |
|
Nesta dica de Java veremos como calcular a equação reduzida da reta quando temos dois pontos pertencentes à esta reta. Não, nessa dica não vamos calcular a equação geral da reta, apenas a equação reduzida. Em outras dicas do site você encontra como como isso pode ser feito. Para relembrar: a equação reduzida da reta é y = mx + n, em que x e y são, respectivamente, a variável independente e a variável dependente; m é o coeficiente angular, e n é o coeficiente linear. Além disso, m e n são números reais. Com a equação reduzida da reta, é possível calcular quais são os pontos que pertencem a essa reta e quais não pertencem. Vamos começar então analisando a seguinte figura, na qual temos dois pontos que pertencem à uma reta: 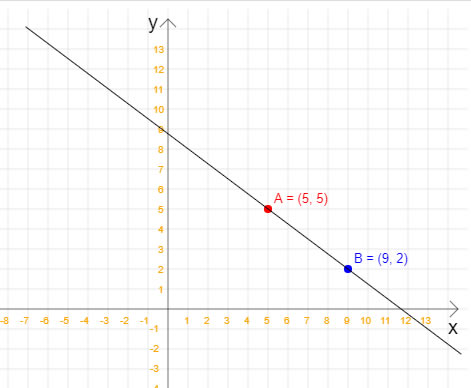 Note que a reta da figura passa pelos pontos A(5, 5) e B(9, 2). Então, uma vez que já temos os dois pontos, já podemos calcular a equação reduzida da reta. Veja o código Java completo para esta tarefa: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
package estudos;
import java.util.Scanner;
public class Estudos{
public static void main(String[] args){
// vamos usar a classe Scanner para ler os dados
Scanner entrada = new Scanner(System.in);
// vamos ler as coordenadas do primeiro ponto
System.out.print("Coordenada x do primeiro ponto: ");
double x1 = Double.parseDouble(entrada.nextLine());
System.out.print("Coordenada y do primeiro ponto: ");
double y1 = Double.parseDouble(entrada.nextLine());
// vamos ler as coordenadas do segundo ponto
System.out.print("Coordenada x do segundo ponto: ");
double x2 = Double.parseDouble(entrada.nextLine());
System.out.print("Coordenada y do segundo ponto: ");
double y2 = Double.parseDouble(entrada.nextLine());
String sinal = "+";
// vamos calcular o coeficiente angular da reta
double m = (y2 - y1) / (x2 - x1);
// vamos calcular o coeficiente linear
double n = y1 - (m * x1);
// coeficiente linear menor que zero? O sinal será negativo
if (n < 0){
sinal = "-";
n = n * -1;
}
// mostra a equação reduzida da reta
System.out.println("Equação reduzida: y = " + m + "x"
+ " " + sinal + " " + n);
System.exit(0);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 5 Coordenada y do primeiro ponto: 5 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 2 Equação reduzida: y = -0,75x + 8,75 Para testarmos se nossa equação reduzida da reta está realmente correta, considere o valor 3 para o eixo x da imagem acima. Ao efetuarmos o cálculo: ---------------------------------------------------------------------- Se precisar de ajuda com o código abaixo, pode me chamar no WhatsApp +55 (62) 98553-6711 (Osmar) ---------------------------------------------------------------------- >> y = (-0.75 * 3) + 8.75 y = 6.5000 temos o valor 6.5 para o eixo y, o que faz com que o novo ponto caia exatamente em cima da reta considerada na imagem. |
Desafios, Exercícios e Algoritmos Resolvidos de Java |
Veja mais Dicas e truques de Java |
Dicas e truques de outras linguagens |
|
Java - Como calcular juros simples e composto - Calculando juros simples e montante na linguagem Java C# - Como retornar a quantidade de elementos que podem ser armazenados na List do C# sem redimensioná-la |
Códigos Fonte |
 Software de Gestão Financeira com código fonte em PHP, MySQL, Bootstrap, jQuery - Inclui cadastro de clientes, fornecedores e ticket de atendimento Software de Gestão Financeira com código fonte em PHP, MySQL, Bootstrap, jQuery - Inclui cadastro de clientes, fornecedores e ticket de atendimentoDiga adeus às planilhas do Excel e tenha 100% de controle sobre suas contas a pagar e a receber, gestão de receitas e despesas, cadastro de clientes e fornecedores com fotos e histórico de atendimentos. Código fonte completo e funcional, com instruções para instalação e configuração do banco de dados MySQL. Fácil de modificar e adicionar novas funcionalidades. Clique aqui e saiba mais |
 Controle de Estoque completo com código fonte em PHP, MySQL, Bootstrap, jQuery - 100% funcional e fácil de modificar e implementar novas funcionalidades Controle de Estoque completo com código fonte em PHP, MySQL, Bootstrap, jQuery - 100% funcional e fácil de modificar e implementar novas funcionalidadesTenha o seu próprio sistema de controle de estoque web. com cadastro de produtos, categorias, fornecedores, entradas e saídas de produtos, com relatórios por data, margem de lucro e muito mais. Código simples e fácil de modificar. Acompanha instruções para instalação e criação do banco de dados MySQL. Clique aqui e saiba mais |
Linguagens Mais Populares |
|
1º lugar: Java |




