Você está aqui: LISP ::: LISP para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como converter Coordenadas Polares para Coordenadas Cartesianas em LISP - LISP para EngenhariaQuantidade de visualizações: 840 vezes |
|
Nesta nossa série de LISP e AutoLISP para Geometria Analítica e Álgebra Linear, mostrarei um código 100% funcional para fazer a conversão entre coordenadas polares e coordenadas cartesianas. Esta operação é muito frequente em computação gráfica e é parte integrante das disciplinas dos cursos de Engenharia (com maior ênfase na Engenharia Civil). Na matemática, principalmente em Geometria e Trigonometria, o Sistema de Coordenadas Polares é um sistema de coordenadas em duas dimensões no qual cada ponto no plano é determinado por sua distância a partir de um ponto de referência conhecido como raio (r) e um ângulo a partir de uma direção de referência. Este ângulo é normalmente chamado de theta (__$\theta__$). Assim, um ponto em Coordenadas Polares é conhecido por sua posição (r, __$\theta__$). Já o sistema de Coordenadas no Plano Cartesiano, ou Espaço Cartesiano, é um sistema que define cada ponto em um plano associando-o, unicamente, a um conjuntos de pontos numéricos. Dessa forma, no plano cartesiano, um ponto é representado pelas coordenadas (x, y), com o x indicando o eixo horizontal (eixo das abscissas) e o y indicando o eixo vertical (eixo das ordenadas). Quando saímos do plano (espaço 2D ou R2) para o espaço (espaço 3D ou R3), temos a inclusão do eixo z (que indica profundidade). Antes de prosseguirmos, veja uma imagem demonstrando os dois sistemas de coordenadas: 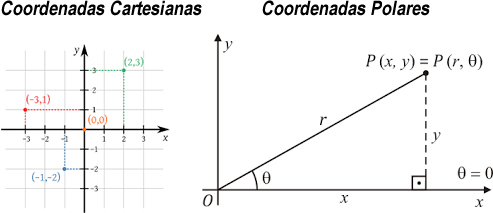 A fórmula para conversão de Coordenadas Polares para Coordenadas Cartesianas é: x = raio × coseno(__$\theta__$) y = raio × seno(__$\theta__$) E aqui está o código LISP completo que recebe as coordenadas polares (r, __$\theta__$) e retorna as coordenadas cartesianas (x, y): ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
; programa LISP que converte Coordenadas Polares
; em Coordenadas Cartesianas
(let((raio)(theta)(graus)(x)(y))
; vamos ler o raio e o ângulo
(princ "Informe o raio: ")
(force-output)
(setq raio (read))
(princ "Informe o theta: ")
(force-output)
(setq theta (read))
(princ "Theta em graus (1) ou radianos (2): ")
(force-output)
(setq graus (read))
; o theta está em graus?
(if(eq graus 1)
(setq theta (* theta (/ pi 180.0)))
)
; fazemos a conversão para coordenadas cartesianas
(setq x (* raio (cos theta)))
(setq y (* raio (sin theta)))
; exibimos o resultado
(format t "As Coordenadas Cartesianas são: (x = ~F, y = ~F)"
x y)
)
Ao executar este código LISP nós teremos o seguinte resultado: Informe o raio: 1 Informe o theta: 1.57 Theta em graus (1) ou radianos (2): 2 As Coordenadas Cartesianas são: (x = 0,00, y = 1,00) |
 Link para compartilhar na Internet ou com seus amigos: |
Veja mais Dicas e truques de LISP |
Dicas e truques de outras linguagens |
|
PHP - Datas e horas em PHP - Como subtrair horas de uma data usando a função mktime() da linguagem PHP |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |
