 |
|
Você está aqui: Lisp ::: Dicas & Truques ::: Strings e Caracteres |
Como pesquisar uma substring em uma string em LISP usando a função search()Quantidade de visualizações: 465 vezes |
|
Nesta dica mostrarei como podemos pesquisar uma palavra ou parte de uma palavra em outra palavra, frase ou texto na linguagem Common Lisp. Para isso nós vamos usar a função search(). Esta função recebe a substring a ser pesquisada e a string na qual a pesquisa será feita. O resultado será o índice da ocorrência do primeiro caractere da substring em caso de sucesso, e o valor nil caso a substring não seja encontrada. Veja o código LISP completo para o exemplo: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
; variáveis que vamos usar no programa
(let ((frase)(palavra)(resultado))
; Vamos pedir para o usuário informar
; uma frase
(princ "Informe uma frase: ")
(force-output)
; atribui o valor lido à variável frase
(setq frase (read-line))
; Vamos pedir para o usuário informar
; uma palavra
(princ "Informe uma palavra: ")
(force-output)
; atribui o valor lido à variável palavra
(setq palavra (read-line))
; agora vamos testar se a palavra está contida
; na frase
(setq resultado (search palavra frase))
(if (eq nil resultado)
(princ "A palavra não está na frase")
(format t "A palavra encontrada no índice: ~D~%"
resultado)
)
)
Ao executarmos este código LISP nós teremos o seguinte resultado: Informe uma frase: Gosto de Java e PHP Informe uma palavra: Java A palavra foi encontrada no índice: 9 |
 Link para compartilhar na Internet ou com seus amigos: |
Lisp ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular a área de um círculo em LISP dado o raio do círculoQuantidade de visualizações: 985 vezes |
A área de um círculo pode ser calculada por meio do produto entre a constante PI e a medida do raio ao quadrado (r2). Comece analisando a figura abaixo: Sendo assim, temos a seguinte fórmula:  Onde A é a área, PI equivale a 3,14 (aproximadamente) e r é o raio do círculo. O raio é a medida que vai do centro até um ponto da extremidade do círculo. O diâmetro é a medida equivalente ao dobro da medida do raio, passando pelo centro do círculo e dividindo-o em duas partes. A medida do diâmetro é 2 * Raio. Veja agora um código Common Lisp completo que calcula a área de um círculo mediante a informação do raio: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
; Vamos definir as variáveis que vamos
; usar no programa
(defvar raio)
(defvar area)
; Este o programa principal
(defun AreaCirculo()
; Vamos ler o raio do círculo
(princ "Informe o raio do círculo: ")
; talvez o seu compilador não precise disso
(force-output)
; atribui o valor lido à variável raio
(setq raio (read))
; calcula a área do círculo
(setq area (* pi (expt raio 2)))
; E mostramos o resultado
(format t "A área do círculo de raio ~F é ~F" raio
area)
)
; Auto-executa a função AreaCirculo()
(AreaCirculo)
Ao executarmos este código nós teremos o seguinte resultado: Informe o raio do círculo: 5 A area do círculo de raio 5 é igual a 78.539816 A circunferência é um conjunto de pontos que estão a uma mesma distância do centro. Essa distância é conhecida como raio. A circunferência é estudada pela Geometria Analítica e, em geral, em um plano cartesiano. O círculo, que é formado pela circunferência e pelos infinitos pontos que preenchem seu interior, é estudado pela Geometria Plana, pois ele ocupa um espaço e pode ter sua área calculada, diferentemente da circunferência. |
Lisp ::: Dicas & Truques ::: Matemática e Estatística |
Como calcular MDC em Lisp usando a função GCDQuantidade de visualizações: 781 vezes |
|
Atualmente a definição de Máximo Divisor Comum (MDC) pode ser assim formalizada: Sejam a, b e c números inteiros não nulos, dizemos que c é um divisor comum de a e b se c divide a (escrevemos c|a) e c divide b (c|b). Chamaremos D(a,b) o conjunto de todos os divisores comum de a e b. Podemos calcular o Máximo Divisor Comum na linguagem Common Lisp usando a função GCD. Esta função aceita um número ilimitado de valores inteiros e retorna seu Máximo Divisor Comum. Veja um trecho de código Common Lisp no qual pedimos para o usuário informar dois números inteiros e, em seguida, fazemos uso da função GCD para retornar o MDC: ---------------------------------------------------------------------- Se precisar de ajuda com o código abaixo, pode me chamar no WhatsApp +55 (62) 98553-6711 (Osmar) ---------------------------------------------------------------------- ; variáveis que vamos usar no programa (let ((num1)(num2)(mdc)) ; Vamos ler o primeiro número (princ "Informe o primeiro número: ") ; talvez o seu compilador não precise disso (force-output) ; atribui o valor lido à variável num1 (setq num1 (read)) ; Vamos ler o segundo número (princ "Informe o segundo número: ") ; talvez o seu compilador não precise disso (force-output) ; atribui o valor lido à variável num2 (setq num2 (read)) ; Vamos obter o MDC dos dois números informados (setq mdc (gcd num1 num2)) ; E mostramos o resultado (format t "O Máximo Divisor Comum é: ~D" mdc) ) Ao executarmos este código Common Lisp nós teremos o seguinte resultado: Informe o primeiro número: 9 Informe o segundo número: 12 O Máximo Divisor Comum é: 3 |
Lisp ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cosseno de um ângulo em LISP e AutoLISP (AutoCAD) usando a função cos() - Calculadora de cosseno em LISPQuantidade de visualizações: 599 vezes |
|
Em geral, quando falamos de cosseno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função cosseno disponível nas linguagens de programação para calcular o cosseno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função cosseno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o cosseno é a razão entre o cateto adjascente e a hipotenusa, ou seja, o cateto adjascente dividido pela hipotenusa. Veja a fórmula: \[\text{Cosseno} = \frac{\text{Cateto adjascente}}{\text{Hipotenusa}} \] Então, se dividirmos 30 por 36.056 (na figura eu arredondei) nós teremos 0.8320, que é a razão entre o cateto adjascente e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.8320. O resultado será 0.5881 (em radianos). Convertendo 0.5881 radianos para graus, nós obtemos 33.69º, que é exatamente o ângulo em graus entre o cateto adjascente e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é cosseno na trigonometria, vamos entender mais sobre a função cos() da Common Lisp e da AutoLISP (a implementação LISP do AutoCAD). Esta função recebe um valor numérico e retorna um valor, também numérico) entre -1 até 1 (ambos inclusos). Veja: ---------------------------------------------------------------------- Se precisar de ajuda com o código abaixo, pode me chamar no WhatsApp +55 (62) 98553-6711 (Osmar) ---------------------------------------------------------------------- (format t "Cosseno de 0 = ~F~%" (cos 0)) (format t "Cosseno de 1 = ~F~%" (cos 1)) (format t "Cosseno de 2 = ~F" (cos 2)) Ao executar este código LISP nós teremos o seguinte resultado: Cosseno de 0 = 1.0 Cosseno de 1 = 0.5403023 Cosseno de 2 = -0.41614684 Note que calculamos os cossenos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função cosseno mostrada abaixo:  |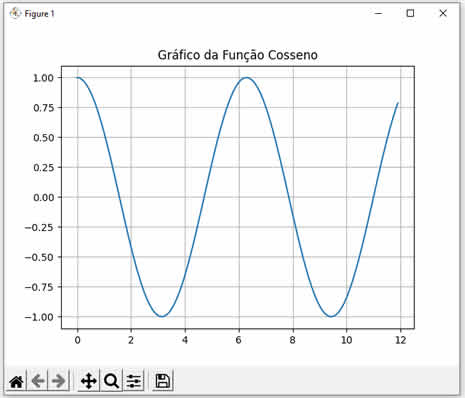
Veja mais Dicas e truques de Lisp |
Dicas e truques de outras linguagens |
Códigos Fonte |
 Software de Gestão Financeira com código fonte em PHP, MySQL, Bootstrap, jQuery - Inclui cadastro de clientes, fornecedores e ticket de atendimentoDiga adeus às planilhas do Excel e tenha 100% de controle sobre suas contas a pagar e a receber, gestão de receitas e despesas, cadastro de clientes e fornecedores com fotos e histórico de atendimentos. Código fonte completo e funcional, com instruções para instalação e configuração do banco de dados MySQL. Fácil de modificar e adicionar novas funcionalidades. Clique aqui e saiba mais |
 Controle de Estoque completo com código fonte em PHP, MySQL, Bootstrap, jQuery - 100% funcional e fácil de modificar e implementar novas funcionalidadesTenha o seu próprio sistema de controle de estoque web. com cadastro de produtos, categorias, fornecedores, entradas e saídas de produtos, com relatórios por data, margem de lucro e muito mais. Código simples e fácil de modificar. Acompanha instruções para instalação e criação do banco de dados MySQL. Clique aqui e saiba mais |
Linguagens Mais Populares |
|
1º lugar: Java |
