 |
|
Você está aqui: Python ::: Dicas & Truques ::: Números Complexos (Complex Numbers) |
Como multiplicar dois números complexos na forma retangular usando PythonQuantidade de visualizações: 433 vezes |
Os números complexos são multiplicados com base na propriedade distributiva, sempre lembrando que um numeral complexo é formado por uma parte real e uma imaginária. Veja:7 + j5 Veja o passo-a-passo para multiplicar dois números complexos na forma retangular: a) (4 + 3j) * (2 + 6j) 8 + 24j + 6j + 18j2 (lembrando que j2 = -1) 8 + 24j + 6j + (18 * (-1)) 8 + 24j + 6j - 18 -10 + 30j Veja agora o código Python completo para este cálculo: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
# Classe para representar um número complexo
class Complexo:
# construtor da classe
def __init__(self, real=0, imaginaria=0):
self.real = real
self.imaginaria = imaginaria
# método principal
def main():
# para guardar os três números complexos
x = Complexo()
y = Complexo()
z = Complexo()
# vamos ler as partes reais e imaginárias dos dois
# números complexos a serem multiplicados
x.real = int(input("Parte real do primeiro numero complexo: "))
x.imaginaria = int(input("Parte imaginaria do primeiro numero complexo: "))
y.real = int(input("Parte real do segundo numero complexo: "))
y.imaginaria = int(input("Parte imaginaria do segundo numero complexo: "))
# obtemos a multiplicação dos números complexos
z = multiplicar(x, y)
# e mostramos o resultado
print("A multiplicacao dos dos dois numeros complexos e: ", end="");
# temos que tratar o sinal
if z.imaginaria < 0:
print("{0} - {1}j".format(z.real, z.imaginaria))
else:
print("{0} + {1}j".format(z.real, z.imaginaria))
# função que recebe dois números complexos e retorna
# a multiplicação de um pelo outro
def multiplicar(x, y):
# criamos o número complexo que será retornado
z = Complexo()
# agora fazemos as multiplicações
z.real = (x.real * y.real) - (x.imaginaria * y.imaginaria)
z.imaginaria = (x.real * y.imaginaria) + (x.imaginaria * y.real)
# retorna o número complexo
return z
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Parte real do primeiro número complexo: 4 Parte imaginária do primeiro número complexo: 3 Parte real do segundo número complexo: 2 Parte imaginária do segundo número complexo: 6 A multiplicação dos dois números complexos é: -10 + 30j |
 Link para compartilhar na Internet ou com seus amigos: |
Python ::: Pandas Python Library (Biblioteca Python Pandas) ::: Input e Output (Entrada e Saída) |
Como usar o método read_csv() do Pandas da linguagem Python para carregar um dataset e retorná-lo como um DataFrameQuantidade de visualizações: 4939 vezes |
|
Quando estamos desenvolvendo soluções em Data Science ou Machine Learning, é comum precisarmos carregar dados contidos em arquivos .csv (nos quais os registros são separados por vírgulas ou ponto-e-vírgula). Para isso podemos usar o método read_csv() da biblioteca Pandas do Python. Veja um exemplo no qual usamos o método read_csv() para carregar um dataset e depois exibir o DataFrame resultante. Para isso usaremos uma amostra de dados de empréstimos aprovados ou recusados. O arquivo .csv pode ser baixado aqui. Eis o código: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
# importamos a biblioteca Pandas
import pandas as pd
def main():
# vamos carregar os dados do arquivo .csv
dados = pd.read_csv("C:\\estudos_python\\emprestimos.csv",
delimiter=";")
# vamos mostrar o DataFrame resultante
print(dados)
if __name__== "__main__":
main()
Quando executarmos este código nós teremos um resultado parecido com:
id nome idade sexo renda valor parc pont ap
0 1 MIGUEL728 24 M 1800 12500 30 34 S
1 2 RAUL46 61 M 2300 10000 24 59 S
2 3 JONAS264 28 M 800 12500 36 59 N
3 4 LETICIA135 71 F 1800 10000 36 13 N
4 5 CARLOS931 60 F 4000 2000 6 10 N
.. ... ... ... ... ... ... ... ... ..
9 96 ANGELA391 91 F 4000 12500 12 33 N
96 97 PEDRO764 50 M 10200 2500 12 1 N
97 98 ADRIANA175 41 F 4000 2000 36 77 S
98 99 ROSA666 42 F 1800 20000 24 74 N
99 100 SARA653 36 F 970 11000 12 42 N
[100 rows x 9 columns]
Note que aqui nós temos uma amostra de 100 registros e cada registro possui 9 colunas. Se você quiser ver todos os 100 registros, troque a linha: print(dados) por print(dados.to_string()) Para finalizar, note que forneci ";" como delimitador para o método read_csv(). |
Python ::: Desafios e Lista de Exercícios Resolvidos ::: Arrays e Matrix (Vetores e Matrizes) |
Exercícios Resolvidos de Python - Como retornar o maior elemento em cada uma das colunas de uma matriz usando PythonQuantidade de visualizações: 1065 vezes |
|
Pergunta/Tarefa: Dada a seguinte matriz: 6 10 4 2 9 7 20 3 1 Sua saída deverá ser parecida com: Maior elemento na coluna 0 é 20 Maior elemento na coluna 1 é 10 Maior elemento na coluna 2 é 7 Veja a resolução comentada deste exercício usando Python: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
# método principal
def main():
# vamos declarar e constuir uma matriz de 3 linhas e três colunas
matriz = [[6, 10, 4], [2, 9, 7], [20, 3, 1]];
# vamos percorrer a matriz e exibir o maior elemento de cada coluna
# começamos com cada coluna
for i in range(len(matriz[0])):
# assumimos que o maior valor é o primeiro dessa coluna
maior = matriz[0][i]
# percorremos todos os elementos desta linha
for j in range(len(matriz)):
# o elemento atual é maior que o maior?
if matriz[j][i] > maior:
# maior assume o valor atual
maior = matriz[j][i]
# exibimos o maior elemento desta coluna
print("Maior elemento na coluna {0} é {1}".format(i, maior))
if __name__== "__main__":
main()
|
Python ::: Python para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como calcular o determinante de uma matriz 3x3 usando a Método de Sarrus em Python - Python para Álgebra LinearQuantidade de visualizações: 5141 vezes |
|
Os estudos da Geometria Analítica e Álgebra Linear envolvem, em boa parte de seus cálculos, a magnitude de vetores, ou seja, o módulo, tamanho, comprimento ou intensidade dos vetores. E isso não é diferente em relação às matrizes. Quando uma matriz é envolvida nos cálculos, com muita frequência precisamos obter o seu determinante, que nada mais é que um número real associado à todas as matrizes quadradas. Nesta dica mostrarei como obter o determinante de uma matriz quadrada de ordem 3, ou seja, três linhas e três colunas, usando o Método de Sarrus (somente matrizes 3x3). Note que é possível obter o mesmo resultado com o Teorema de Laplace, que não está restrito às matrizes quadradas de ordem 3. Veja também que não considerei as propriedades do determinante, o que, em alguns casos, simplifica muito os cálculos. Então, vamos supor a seguinte matriz 3x3: 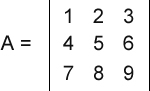 O primeiro passo é copiarmos a primeira e a segunda colunas para o lado direito da matriz. Assim: 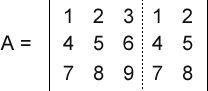 Agora dividimos a matriz em dois conjuntos: três linhas diagonais descendentes e três linhas diagonais ascendentes: 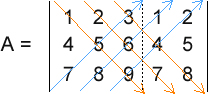 Agora é só efetuar cálculos. Multiplicamos e somamos os elementos de cada conjunto, subtraindo o segundo conjunto do primeiro. Veja: (1 x 5 x 9 + 2 x 6 x 7 + 3 x 4 x 8) - (7 x 5 x 3 + 8 x 6 x 1 + 9 x 4 x 2) = 0 Como podemos ver, o determinante dessa matriz é 0. E agora veja o código Python no qual declaramos e instanciamos uma matriz 3x3, em seguida, calculamos o seu determinante: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
# importamos a bibliteca NumPy
import numpy as np
# função principal do programa
def main():
# vamos criar uma matriz 3x3
m = np.array([(1, 2, 3), (2, 5, 2), (1, 3, 1)])
# calcula o determinante usando a Regra de Sarrus
det = ((m[0][0] * m[1][1] * m[2][2]) + (m[0][1]
* m[1][2] * m[2][0]) + (m[0][2] * m[1][0] * m[2][1])) - ((m[2][0]
* m[1][1] * m[0][2]) + (m[2][1] * m[1][2] * m[0][0]) + (m[2][2]
* m[1][0] * m[0][1]))
# mostramos o resultado
print("O determinante da matriz é: %f" % det)
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: O determinante da matriz é: 2.0 É possível também obter o determinante de uma matriz (não restrita à dimensão 3x3) usando o método linalg.det() da biblioteca NumPy do Python. Veja o código a seguir: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
# importamos a bibliteca NumPy
import numpy as np
# função principal do programa
def main():
# vamos criar uma matriz 3x3
m = np.array([(1, 2, 3), (2, 5, 2), (1, 3, 1)])
# calcula o determinante usando apenas NumPy
det = np.linalg.det(m)
# mostramos o resultado
print("O determinante da matriz é: %f" % det)
if __name__== "__main__":
main()
Veja que usei a mesma matriz e, usando apenas o método linalg.det() nós obtemos o mesmo resultado. |
Desafios, Exercícios e Algoritmos Resolvidos de Python |
Veja mais Dicas e truques de Python |
Dicas e truques de outras linguagens |
Códigos Fonte |
 Software de Gestão Financeira com código fonte em PHP, MySQL, Bootstrap, jQuery - Inclui cadastro de clientes, fornecedores e ticket de atendimentoDiga adeus às planilhas do Excel e tenha 100% de controle sobre suas contas a pagar e a receber, gestão de receitas e despesas, cadastro de clientes e fornecedores com fotos e histórico de atendimentos. Código fonte completo e funcional, com instruções para instalação e configuração do banco de dados MySQL. Fácil de modificar e adicionar novas funcionalidades. Clique aqui e saiba mais |
 Controle de Estoque completo com código fonte em PHP, MySQL, Bootstrap, jQuery - 100% funcional e fácil de modificar e implementar novas funcionalidadesTenha o seu próprio sistema de controle de estoque web. com cadastro de produtos, categorias, fornecedores, entradas e saídas de produtos, com relatórios por data, margem de lucro e muito mais. Código simples e fácil de modificar. Acompanha instruções para instalação e criação do banco de dados MySQL. Clique aqui e saiba mais |
Linguagens Mais Populares |
|
1º lugar: Java |
