Você está aqui: Python ::: Tkinter GUI Toolkit ::: Canvas |
Como usar o componente Canvas em suas aplicações Tkinter PythonQuantidade de visualizações: 1426 vezes |
|
O que é o objeto Canvas do Tkinter? O controle Canvas é uma área retangular usada com o propósito de desenhar gráficos, tais como linhas, círculos, retângulos, polígonos, etc. Além disso, o objeto Canvas permite a inserção de imagens, texto, frames e até controles visuais tais como botões, labels, caixas de texto, entre outros. Como criar um objeto Canvas no Tkinter? Em sua forma mais simples, um controle Canvas é criado por meio de uma chamada ao construtor Canvas(), fornecendo o nome de seu componente pai e opções de personalização do controle. Veja o código abaixo: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# vamos importar o módulo Tkinter
from tkinter import *
from tkinter.ttk import *
# método principal
def main():
# cria a janela principal da aplicação
janela_principal = Tk()
# define as dimensões da janela
janela_principal.geometry("400x350")
# define o título da janela
janela_principal.title("Uso do controle Canvas")
# vamos criar o objeto Canvas
canvas = Canvas(janela_principal, bg="white", width=400, height=350)
# colocamos o Canvas na janela principal
canvas.grid(row=0, column=0)
# agora vamos desenhar um círculo no Canvas
canvas.create_oval(40, 40, 150, 150)
# entramos no loop de eventos
janela_principal.mainloop()
if __name__== "__main__":
main()
Ao executar esta aplicação Tkinter Python nós teremos o seguinte resultado: 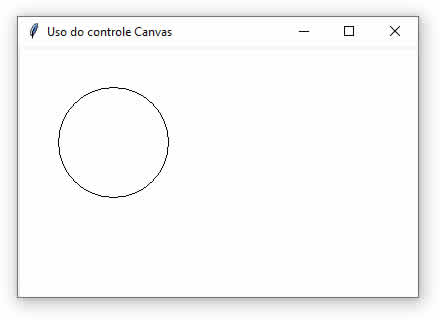 |
|
|
Python ::: Desafios e Lista de Exercícios Resolvidos ::: Python Básico |
Exercício Resolvido de Python - Ler três números inteiros e indicar se eles estão em ordem crescente ou decrescenteQuantidade de visualizações: 847 vezes |
|
Pergunta/Tarefa: Escreva um programa Python que pede para o usuário informar três números inteiros e informa se eles estão em ordem crescente ou decrescente. Se os números estiverem em ordem crescente, escreva "Ordem Crescente". Se estiverem em ordem decrescente, escreva "Ordem Decrescente". Do contrário escreva "Sem ordem definida". Sua saída deverá ser parecida com: Primeiro número: 4 Segundo número: 8 Terceiro número: 11 Ordem Crescente Veja a resolução comentada deste exercício em Python: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# função principal do programa
def main():
# vamos ler três números do usuário
a = int(input("Primeiro número: "))
b = int(input("Segundo número: "))
c = int(input("Terceiro número: "))
# os números estão em ordem crescente?
if a < b and b < c:
print("Ordem Crescente")
# os números estão em ordem decrescente?
elif a > b and b > c:
print("Ordem Decrescente")
# sem ordem definida
else:
print("Sem ordem definida")
if __name__== "__main__":
main()
|
Python ::: Dicas & Truques ::: Lista (List) |
Como pesquisar um item em uma lista Python e retornar seu índice usando a função index()Quantidade de visualizações: 10931 vezes |
|
Em algumas situações nós precisamos pesquisar um item em uma List do Python e retornar o índice de sua primeira ocorrência. Para isso nós podemos usar o método index(), que aceita uma string, um number, um object, etc, e retorna o índice da primeira posição do item dentro da lista. Veja um exemplo de seu uso: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
"""
Este exemplo mostra como pesquisar um item em
uma lista. Se o item for encontrado, seu índice é
retornado. Do contrário uma exceção do tipo ValueError
é levantada.
"""
def main():
# cria uma lista de inteiros
valores = [2, 5, 12, 2, 3, 32, 18]
try:
indice = valores.index(13)
except ValueError:
print("O valor pesquisado nao foi encontrado")
else:
print("O valor foi encontrado no índice", indice)
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: O valor pesquisado não foi encontrado. Note que no exemplo nós usamos um bloco try..except para tratar a exceção ValueError, disparada quando o item pesquisado por meio da função index() não for encontrado na List. Veja: ---------------------------------------------------------------------- Se precisar de ajuda para ajustar o código abaixo de acordo com as suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar) Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar a manter o site livre de anúncios. Ficaremos eternamente gratos ;-) Nosso PIX é: osmar@arquivodecodigos.com.br ---------------------------------------------------------------------- Exception has occurred: ValueError 13 is not in list |
Python ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como embaralhar os elementos de um array em Python usando random.shuffle()Quantidade de visualizações: 1171 vezes |
|
Nesta dica mostrarei como podemos embaralhar a ordem dos elementos de uma lista do Python. Para isso usaremos o método shuffle() do módulo random. Este método muda a ordem dos elementos no vetor original. Veja o código completo para o exemplo: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# vamos importar o módulo random
import random
# função principal do programa
def main():
# vamos criar uma lista de números inteiros
numeros = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
# vamos mostrar o vetor original
print("Ordem original: {0}".format(numeros))
# agora vamos embaralhar a ordem dos elementos da lista
random.shuffle(numeros)
# e mostramos o resultado
print("Após o embaralhamento: {0}".format(numeros))
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Ordem original: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] Após o embaralhamento: [3, 10, 6, 8, 9, 5, 7, 4, 1, 2] |
Python ::: Python para Engenharia ::: Física - Hidrodinâmica |
Como representar a Equação da Continuidade em Python - Python para HidrodinâmicaQuantidade de visualizações: 298 vezes |
|
O que é a Equação da Continuidade? A Hidrodinâmica é a parte da Física que estuda os fluidos em movimento, enquanto a Equação da Continuidade, que é parte da Hidrodinâmica, determina o fluxo de um fluido através de uma área. Esta equação está muito presente quando o assunto é Dinâmica dos Fluidos ou Mecânica dos Fluidos. A Equação da Continuidade é uma consequência direta da Lei da Conservação da Massa. Por meio dessa propriedade, podemos dizer que a quantidade de massa de fluido que atravessa o tubo é a mesma na entrada e na saída. Para melhor entendimento veja a seguinte figura:  Sabendo que a quantidade de água que entra na mangueira deve ser igual à mesma quantidade que sai, ao colocarmos o dedo na saída da mangueira, nós estamos estreitando a área da vazão, o que, consequentemente, aumenta a velocidade da água. Qual é a Fórmula da Equação da Continuidade? Antes de passarmos ao código Python, vamos revisar a Fórmula da Equação da Continuidade. Veja: \[ A_1 \cdot \text{v}_1 = A_2 \cdot \text{v}_2 \] Por meio dessa equação nós entramos com três valores e obtemos um quarto valor. Não se esqueça de que as velocidades são dadas em metros por segundo e as áreas são dadas em metros quadrados (de acordo com o SI - Sistema Internacional de Medidas). Tenha a certeza de efetuar as devidas conversões para não obter resultados incorretos. Vamos escrever código Python agora? A Equação da Continuidade em código Python Para exemplificar como podemos representar a Equação da Continuidade em Python, vamos resolver o seguinte problema? 1) Um fluido escoa a 2 m/s em um tubo de área transversal igual a 200 mm2. Qual é a velocidade desse fluido ao sair pelo outro lado do tubo, cuja área é de 100 mm2? a) 20 m/s b) 4 m/s c) 0,25 m/s d) 1,4 m/s e) 0,2 m/s Note que a velocidade já está em metros por segundo, mas as áreas foram dadas em milímetros quadrados. Por essa razão nós deveremos converter milímetros quadrados em metros quadrados. Veja o código Python completo para a resolução deste exercício de Equação da Continuidade: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# função principal do programa
def main():
# vamos solicitar os dados de entrada
v1 = float(input("Velocidade de entrada (m/s): "))
a1 = float(input("Área de entrada (milímetros quadrados): "))
a2 = float(input("Área de saída (milímetros quadrados): "))
# vamos converter as áreas em milímetros quadrados
# para metros quadrados
a1 = a1 / 1000000
a2 = a2 / 1000000
# agora calculamos a velocidade de saída
v2 = (a1 * v1) / a2
# e mostramos o resultado
print("A velocidade de saída é: {0} m/s".format(v2))
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Velocidade de entrada (m/s): 2 Área de entrada (milímetros quadrados): 200 Área de saída (milímetros quadrados): 100 A velocidade de saída é: 4.0 m/s Portanto, a velocidade do fluido na saída do tubo é de 4 m/s. |
Python ::: Fundamentos da Linguagem ::: Estruturas de Controle |
Apostila Python para iniciantes - Como exibir os números pares de 0 a 20 usando o laço for da linguagem PythonQuantidade de visualizações: 13633 vezes |
|
Nesta dica mostrarei como podemos usar o laço for da linguagem Python para exibir os números pares de 0 a 20. Note que usaremos os parâmetros start (valor inicial da variável de controle), stop (valor final da variável de controle, não incluído) e step (que especifica o valor de incremento da variável de controle. Veja o código completo para o exemplo: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# função principal do programa
def main():
for i in range(0, 21, 2):
print(i, end = " ")
if __name__== "__main__":
main()
Ao executar este código nós teremos o seguinte resultado: 0 2 4 6 8 10 12 14 16 18 20 |
Python ::: Fundamentos da Linguagem ::: Estruturas de Controle |
Como criar um laço while() infinito na linguagem PythonQuantidade de visualizações: 10013 vezes |
|
Nesta dica eu mostrarei como é possível criar um laço (loop) while infinito em Python. Esta técnica é útil para as situações nas quais queremos interagir com o usuário do nosso programa até que um determinado valor seja informado. No exemplo abaixo temos um laço while() que será executado até que o texto "fim" seja informado pelo usuário. Veja o código completo: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
def main():
while True:
frase = input("Digite uma frase: ");
print("Você digitou: ", frase)
# vamos sair do laço
if frase == "fim":
print("Você acaba de sair do laço while()")
break
if __name__== "__main__":
main()
Ao executar este código nós teremos o seguinte resultado: Digite uma frase: Estou estudando Python Você digitou: Estou estudando Python Digite uma frase: Preciso viajar amanhã Você digitou: Preciso viajar amanhã Digite uma frase: fim Você digitou: fim Você acaba de sair do laço while() |
Python ::: Dicas & Truques ::: Formatação de datas, strings e números |
Python para matemática - Como definir a precisão (casas decimais) na exibição de um valor de ponto-flutuante em PythonQuantidade de visualizações: 14993 vezes |
|
Este trecho de código mostra como definir a precisão com que um número de ponto-flutuante será exibido. Atenção: Arredondamentos podem ocorrer dependendo da redução das casas decimais. Veja o código Python completo para a dica: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
def main():
valor = 43.13985765
# com dois dígitos
print("O valor e %.2f" % valor)
# com três dígitos
print("O valor e %.3f" % valor)
# com um dígito
print("O valor e %.1f" % valor)
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: O valor é 43.14 O valor é 43.140 O valor é 43.1 |
Python ::: Desafios e Lista de Exercícios Resolvidos ::: Arrays e Matrix (Vetores e Matrizes) |
Exercícios Resolvidos de Python - Escreva um programa Python para mover todos os zeros para o final do vetor, sem alterar a ordem dos elementos já presentes no arrayQuantidade de visualizações: 1787 vezes |
|
Pergunta/Tarefa: Dado o seguinte vetor de inteiros: # vamos declarar e construir um vetor de 8 inteiros valores = [0, 3, 0, 5, 7, 4, 0, 9] Sua saída deverá ser parecida com: Vetor na ordem original: 0 3 0 5 7 4 0 9 Vetor com os zeros deslocados para o final: 3 5 7 4 9 0 0 0 Veja a resolução comentada deste exercício usando Python: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# método principal
def main():
# vamos declarar e construir um vetor de 8 inteiros
valores = [0, 3, 0, 5, 7, 4, 0, 9]
# vamos mostrar o vetor na ordem original
print("Vetor na ordem original:\n")
for i in range(len(valores)):
print("%d " % valores[i], end="")
# vamos inicializar j como 0 para que ele aponte para
# o primeiro elemento do vetor
j = 0
# agora o laço for percorre todos os elementos do vetor,
# incrementanto a variável i e deixando o j em 0
for i in range(len(valores)):
# encontramos um valor que não é 0
if(valores[i] != 0):
# fazemos a troca entre os elementos nos índices
# i e j
temp = valores[i]
valores[i] = valores[j]
valores[j] = temp
# e avançamos o j para o elemento seguinte
j = j + 1
# agora mostramos o resultado
print("\n\nVetor com os zeros deslocados para o final:\n")
for i in range(len(valores)):
print("%d " % valores[i], end="")
if __name__== "__main__":
main()
Não se esqueça: A resolução do exercício deve ser feita sem a criação de um vetor, array ou lista adicional, e os elementos diferentes de zero devem permanecer na mesma ordem que eles estavam antes. |
Mais Desafios de Programação e Exercícios e Algoritmos Resolvidos de Python |
Veja mais Dicas e truques de Python |
Dicas e truques de outras linguagens |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





