 |
|
Você está aqui: Python ::: Tkinter GUI Toolkit ::: Frame |
Como usar o controle Frame do Tkinter Python para organizar os componentes visuais de uma janela ou formulárioQuantidade de visualizações: 1876 vezes |
|
Além do gerenciador Grid que estamos acostumados a usar no Tkinter Python, temos também à nossa disposição o controle Frame. O componente Frame é um controle que é exibido como um retângulo e usado para organizar outros componentes, tanto visualmente quanto a nível de código. Este controle possui vários atributos, tais como tamanho, espaço interno e bordas. Veja um trecho de código no qual temos uma janela Tk principal, um controle Frame e, dentro do frame, três botões Button. Note como manipulei o espaço interno da frame e os espaços entre os botões para gerar um layout agradável aos olhos do usuário: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
# vamos importar o módulo Tkinter
from tkinter import *
from tkinter.ttk import *
# método principal
def main():
# vamos criar a tela de login
janela = Tk()
# vamos definir o tamanho da janela
janela.geometry("300x200")
# o titulo da janela
janela.title("Uso do controle Frame")
# vamos criar o componente Frame
frame = Frame(janela)
# vamos definir o espaço interno do frame
frame['padding'] = 15
# e colocamos o frame na linha 0 e coluna 0 da janela principal
frame.grid(column=0, row=0)
# colocamos o primeiro botão na coluna 0 e linha 0
btn_1 = Button(frame, text="Botão 1")
btn_1.grid(column=0, row=0, padx=5, pady=0)
# colocamos o segundo botão na coluna 1 e linha 0
btn_2 = Button(frame, text="Botão 2")
btn_2.grid(column=1, row=0, padx=5, pady=0)
# colocamos o terceiro botão na coluna 2 e linha 0
btn_3 = Button(frame, text="Botão 3")
btn_3.grid(column=2, row=0, padx=5, pady=0)
# entramos no loop de eventos
janela.mainloop()
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado:  |
 Link para compartilhar na Internet ou com seus amigos: |
Python ::: Dicas & Truques ::: Strings e Caracteres |
Como testar se o primeiro caractere de cada palavra em uma string Python é o único em letra maiúscula usando a função istitle()Quantidade de visualizações: 8653 vezes |
|
Nesta dica mostrarei como podemos usar a função istitle() da linguagem Python para verificar se o primeiro caractere de cada palavra em uma frase ou texto é o único caractere em letra maiúscula. Se o teste for verdadeiro o retorno é true, caso contrário o retorno é false. Veja o exemplo completo: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
def main():
frase = "Gosto De Programar Em Python"
if frase.istitle():
print("O primeiro caractere de cada palavra é maiusculo")
else:
print("O teste não resultou verdadeiro")
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: O primeiro caractere de cada palavra é maiusculo. |
Python ::: Python para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como calcular o determinante de uma matriz 3x3 usando a Método de Sarrus em Python - Python para Álgebra LinearQuantidade de visualizações: 5131 vezes |
|
Os estudos da Geometria Analítica e Álgebra Linear envolvem, em boa parte de seus cálculos, a magnitude de vetores, ou seja, o módulo, tamanho, comprimento ou intensidade dos vetores. E isso não é diferente em relação às matrizes. Quando uma matriz é envolvida nos cálculos, com muita frequência precisamos obter o seu determinante, que nada mais é que um número real associado à todas as matrizes quadradas. Nesta dica mostrarei como obter o determinante de uma matriz quadrada de ordem 3, ou seja, três linhas e três colunas, usando o Método de Sarrus (somente matrizes 3x3). Note que é possível obter o mesmo resultado com o Teorema de Laplace, que não está restrito às matrizes quadradas de ordem 3. Veja também que não considerei as propriedades do determinante, o que, em alguns casos, simplifica muito os cálculos. Então, vamos supor a seguinte matriz 3x3:  O primeiro passo é copiarmos a primeira e a segunda colunas para o lado direito da matriz. Assim:  Agora dividimos a matriz em dois conjuntos: três linhas diagonais descendentes e três linhas diagonais ascendentes:  Agora é só efetuar cálculos. Multiplicamos e somamos os elementos de cada conjunto, subtraindo o segundo conjunto do primeiro. Veja: (1 x 5 x 9 + 2 x 6 x 7 + 3 x 4 x 8) - (7 x 5 x 3 + 8 x 6 x 1 + 9 x 4 x 2) = 0 Como podemos ver, o determinante dessa matriz é 0. E agora veja o código Python no qual declaramos e instanciamos uma matriz 3x3, em seguida, calculamos o seu determinante: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
# importamos a bibliteca NumPy
import numpy as np
# função principal do programa
def main():
# vamos criar uma matriz 3x3
m = np.array([(1, 2, 3), (2, 5, 2), (1, 3, 1)])
# calcula o determinante usando a Regra de Sarrus
det = ((m[0][0] * m[1][1] * m[2][2]) + (m[0][1]
* m[1][2] * m[2][0]) + (m[0][2] * m[1][0] * m[2][1])) - ((m[2][0]
* m[1][1] * m[0][2]) + (m[2][1] * m[1][2] * m[0][0]) + (m[2][2]
* m[1][0] * m[0][1]))
# mostramos o resultado
print("O determinante da matriz é: %f" % det)
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: O determinante da matriz é: 2.0 É possível também obter o determinante de uma matriz (não restrita à dimensão 3x3) usando o método linalg.det() da biblioteca NumPy do Python. Veja o código a seguir: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
# importamos a bibliteca NumPy
import numpy as np
# função principal do programa
def main():
# vamos criar uma matriz 3x3
m = np.array([(1, 2, 3), (2, 5, 2), (1, 3, 1)])
# calcula o determinante usando apenas NumPy
det = np.linalg.det(m)
# mostramos o resultado
print("O determinante da matriz é: %f" % det)
if __name__== "__main__":
main()
Veja que usei a mesma matriz e, usando apenas o método linalg.det() nós obtemos o mesmo resultado. |
Python ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o diâmetro, a circunferência e a área de um círculo dado o raio em Python - Python para GeometriaQuantidade de visualizações: 4871 vezes |
|
O círculo é uma figura geométrica plana e que possui quatro características: seu raio, seu diâmetro, sua circunferência e sua área. Aqui já podemos aproveitar e relembrar a diferença entre o círculo e a circunferência. O círculo é o conjunto de pontos resultantes da união entre uma circunferência e seus pontos internos, ou seja, o círculo é a área cuja delimitação é uma circunferência. É importante observar que alguns autores tratam o círculo como uma circunferência. Assim, para estes autores, calcular a circunferência de um círculo equivale a calcular o perímetro da circunferência. Veja a figura a seguir para relembrar o que é o raio de um círculo:  Nesta dica mostrarei como podemos usar Python para calcular o diâmetro, a circunferência e a área de um círculo tendo apenas o raio como informação. Antes, porém, vamos às formulas. Sabendo que r é o raio, temos: \[\text{Diâmetro d} = 2 \times r \] \[\text{Circunferência C} = 2 \times \pi \times r \] \[\text{Área A} = \pi \times r^2 \] Agora vamos ver o código Python que solicita ao usuário que informe o raio do círculo e mostra o diâmetro, a circunferência e a área: ----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------
import math as math
def main():
# vamos ler o raio do círculo
raio = float(input("Informe o raio do círculo: "))
# vamos achar o diâmetro do círculo
diametro = 2 * raio
# agora calculamos a circunferência
circunferencia = 2 * math.pi * raio
# finalmente calculamos a área do círculo
area = math.pi * math.pow(raio, 2)
# vamos mostrar os resultados
print("O diâmetro do círculo é:", diametro)
print("A circunferência do círculo é:", circunferencia)
print("A área do círculo é:", area)
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Informe o raio do círculo: 10 O diâmetro do círculo é: 20.0 A circunferência do círculo é: 62.83185307179586 A área do círculo é: 314.1592653589793 Lembre-se de que a área é em centímetros quadrados, metros quadrados, etc. |
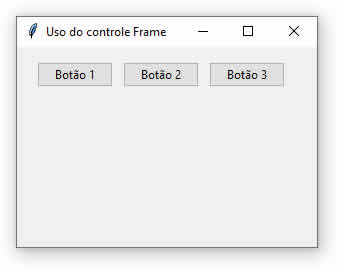Desafios, Exercícios e Algoritmos Resolvidos de Python |
Veja mais Dicas e truques de Python |
Dicas e truques de outras linguagens |
Códigos Fonte |
 Software de Gestão Financeira com código fonte em PHP, MySQL, Bootstrap, jQuery - Inclui cadastro de clientes, fornecedores e ticket de atendimentoDiga adeus às planilhas do Excel e tenha 100% de controle sobre suas contas a pagar e a receber, gestão de receitas e despesas, cadastro de clientes e fornecedores com fotos e histórico de atendimentos. Código fonte completo e funcional, com instruções para instalação e configuração do banco de dados MySQL. Fácil de modificar e adicionar novas funcionalidades. Clique aqui e saiba mais |
 Controle de Estoque completo com código fonte em PHP, MySQL, Bootstrap, jQuery - 100% funcional e fácil de modificar e implementar novas funcionalidadesTenha o seu próprio sistema de controle de estoque web. com cadastro de produtos, categorias, fornecedores, entradas e saídas de produtos, com relatórios por data, margem de lucro e muito mais. Código simples e fácil de modificar. Acompanha instruções para instalação e criação do banco de dados MySQL. Clique aqui e saiba mais |
Linguagens Mais Populares |
|
1º lugar: Java |
