 |
|
||||
Você está aqui: Python ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como testar se um ponto está dentro de um círculo em Python - Desenvolvimento de Games com PythonQuantidade de visualizações: 1163 vezes |
|
Quando estamos trabalhando com computação gráfica, geometria e trigonometria ou desenvolvimento de jogos em Python, é comum precisarmos verificar se um determinado ponto (uma coordenada x, y) está contido dentro de um círculo. Para melhor entendimento, veja a imagem a seguir: 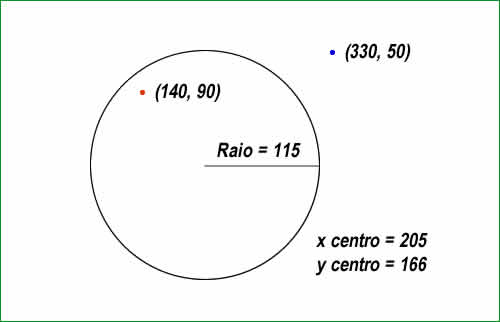 Veja que temos um círculo com raio igual a 115 e com centro nas coordenadas (x = 205; y = 166). Temos também dois pontos. O ponto vermelho está nas coordenadas (x = 140; y = 90) e o ponto azul está nas coordenadas (x = 330; y = 500. Como podemos ver na imagem, o ponto vermelho está dentro do círculo, enquanto o ponto azul está fora. E nosso intenção nesta dica é escrever o código Python que permite fazer essa verificação. Tenha em mente que está técnica é muito útil para o teste de colisões no desenvolvimento de games. Veja o código completo para o exemplo: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# vamos importar o módulo Math
import math
# vamos declarar a classe Circulo
class Circulo:
# construtor da classe
def __init__(self, xc, yc, raio):
self.xc = xc
self.yc = yc
self.raio = raio
# agora vamos declarar a classe Ponto
class Ponto:
def __init__(self, x, y):
self.x = x # coordenada x
self.y = y # coordenada y
# método principal
def main():
# vamos criar um objeto Circulo
c = Circulo(205, 166, 115)
# vamos criar um objeto Ponto
p = Ponto(140, 90)
# vamos verificar se o ponto está dentro do
# círculo
dx = p.x - c.xc;
dy = p.y - c.yc;
if((math.pow(dx, 2) + math.pow(dy, 2)) < math.pow(c.raio, 2)):
print("O ponto está dentro do círculo")
else:
print("O ponto NÃO está dentro do círculo")
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: O ponto está dentro do círculo. Experimente com círculos de raios e coordenadas centrais diferentes e também com pontos em várias coordenadas e veja como os resultados são interessantes. |
 Link para compartilhar na Internet ou com seus amigos: |
Python ::: Dicas & Truques ::: Strings e Caracteres |
Como retornar o código ASCII ou Unicode de um caractere em Python usando a função ord()Quantidade de visualizações: 13491 vezes |
|
Nesta dica vou mostrar como é possível usar a função ord() da linguagem Python para retornar o código ASCII ou Unicode de um determinado caractere (letra, dígito ou símbolo). Veja o exemplo completo: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
def main():
print("O codigo ASCII ou Unicode para o caractere A é",
ord('A'))
if __name__== "__main__":
main()
Ao executarmos este código nós teremos o seguinte resultado: O codigo ASCII ou Unicode para o caractere A é 65 |
Python ::: Desafios e Lista de Exercícios Resolvidos ::: Hidrologia e Hidráulica |
Exercícios Resolvidos de Python - Qual seria a vazão (m3/h) de saída para uma bacia hidrográfica "completamente impermeável", com área de 60 km2, sob uma chuva constanteQuantidade de visualizações: 369 vezes |
|
Pergunta/Tarefa: 1) Qual seria a vazão (m3/h) de saída para uma bacia hidrográfica "completamente impermeável", com área de 60 km2, sob uma chuva constante à taxa de 10 mm/h? A) 180.000 m3/h B) 6.000 m3/h C) 600.000 m3/h D) 60.000 m3/h E) 600.000.000 m3/h Sua saída deve ser parecida com: Área da bacia em km2: 60 Precipitação em mm/h: 10 A vazão é: 600000.0 m3/h O primeiro passo para resolver esta questão é relembrar a fórmula da vazão: \[\text{Q} = \text{A} \cdot \text{v}\] Onde: Q = vazão em m3/s, m3/h, etc; A = área da bacia m2, km2, etc. v = a taxa da chuva, ou seja, a precipitação em mm/s, mm/h, etc. A maior dificuldade aqui é a conversão das unidades, pois o exercício nos pede a vazão em m3/h. Por essa razão temos que converter a área para metros quadrados e a precipitação em milímetros para precipitação em metros. Então, hora de vermos a resolução comentada deste exercício usando Python: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# função principal do programa
def main():
# vamos ler a área da bacia em km2
area = float(input("Área da bacia em km2: "))
# vamos ler a precipitação em milímetros por hora
precipitacao = float(input("Precipitação em mm/h: "))
# vamos calcular a vazão em metros cúbicos por hora
# primeiro convertemos a área para metros quadrados
area = area * 1000000.0
# agora convertemos milímetros para metros
precipitacao = precipitacao / 1000.0
# e calculamos a vazão
vazao = area * precipitacao
# e mostramos o resultado
print("A vazão é: {0} m3/h".format(vazao))
if __name__== "__main__":
main()
|
Python ::: Dicas & Truques ::: Data e Hora |
Como construir uma data em Python usando o construtor da classe datetimeQuantidade de visualizações: 6828 vezes |
|
Nesta dica mostrarei como podemos usar o construtor da classe datetime do Python para construir e retornar uma nova data. Note que estou fornecendo a data para construtor da classe datetime usando o ano, o mês e o dia. Veja o código Python completo para o exemplo: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
from datetime import datetime
# função principal do programa
def main():
# vamos definir o dia, mês e ano
dia = 20
mes = 4
ano = 1980
# Constrói um datetime (ano, mês, dia)
data = datetime(ano, mes, dia)
# Exibe o conteúdo do datetime
print("A data construída foi {0}".format(data))
# Obtém o ano da data recém-criada
print("O ano da data construída foi: {0}".format(data.year))
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: A data construída foi 1980-04-20 00:00:00 O ano da data construída foi: 1980 |
Python ::: Python para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como calcular a norma ou módulo de vetores nos espaços R2 e R3 usando Python - Geometria Analítica e Álgebra Linear usando PythonQuantidade de visualizações: 3783 vezes |
|
Em Geometria Analítica e Álgebra Linear, a magnitude, norma, comprimento, tamanho ou módulo (também chamado de intensidade na Física) de um vetor é o seu comprimento, que pode ser calculado por meio da distância de seu ponto final a partir da origem, no nosso caso (0,0). Considere o seguinte vetor no plano, ou seja, no espaço bidimensional, ou R2: \[\vec{v} = \left(7, 6\right)\] Aqui este vetor se inicia na origem (0, 0) e vai até as coordenadas (x = 7) e (y = 6). Veja sua plotagem no plano 2D:  Note que na imagem já temos todas as informações que precisamos, ou seja, o tamanho desse vetor é 9 (arredondado) e ele faz um ângulo de 41º (graus) com o eixo x positivo. Em linguagem mais adequada da trigonometria, podemos dizer que a medida do cateto oposto é 6, a medida do cateto adjacente é 7 e a medida da hipotenusa (que já calculei para você) é 9. Note que já mostrei também o ângulo theta (__$\theta__$) entre a hipotenusa e o cateto adjacente, o que nos dá a inclinação da reta representada pelos pontos (0, 0) e (7, 6). Relembrando nossas aulas de trigonometria nos tempos do colegial, temos que o quadrado da hipotenusa é a soma dos quadrados dos catetos, ou seja, o Teorema de Pitágoras: \[a^2 = b^2 + c^2\] Como sabemos que a potenciação é o inverso da radiciação, podemos escrever essa fórmula da seguinte maneira: \[a = \sqrt{b^2 + c^2}\] Passando para os valores x e y que já temos: \[a = \sqrt{7^2 + 6^2}\] Podemos comprovar que o resultado é 9,21 (que arredondei para 9). Não se esqueça da notação de módulo ao apresentar o resultado final: \[\left|\vec{v}\right| = \sqrt{7^2 + 6^2}\] E aqui está o código Python que nos permite informar os valores x e y do vetor e obter o seu comprimento, tamanho ou módulo: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# função principal do programa
def main():
# vamos ler os valores x e y
x = float(input("Informe o valor de x: "))
y = float(input("Informe o valor de y: "))
# vamos calcular a norma do vetor
norma = math.sqrt(math.pow(x, 2) + math.pow(y, 2))
# mostra o resultado
print("A norma do vetor é: %0.2f" % norma)
if __name__== "__main__":
main()
Ao executar este código nós teremos o seguinte resultado: Informe o valor de x: 7 Informe o valor de y: 6 A norma do vetor é: 9.22 Novamente note que arredondei o comprimento do vetor para melhor visualização no gráfico. Para calcular a norma de um vetor no espaço, ou seja, no R3, basta acrescentar o componente z no cálculo. |
Python ::: Desafios e Lista de Exercícios Resolvidos ::: Python Básico |
Exercícios Resolvidos de Python - Lendo a idade de um nadador e classificando sua categoria como infantil, juvenil, adolescente, adulto ou sêniorQuantidade de visualizações: 377 vezes |
|
Pergunta/Tarefa: Escreva um programa Python que solicita a idade de um nadador e classifica sua categoria de acordo com as seguintes regras: a) De 5 a 7 anos - Infantil; b) De 8 a 10 anos - Juvenil; c) De 11 a 15 anos - Adolescente; d) De 16 a 30 anos - Adulto; e) Acima de 30 anos - Sênior. Sua saída deverá ser parecida com: Informe sua idade: 19 Sua categoria é Adulto Veja a resolução comentada deste exercício usando Python: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# vamos solicitar a idade do nadador
idade = int(input("Informe sua idade: "))
# vamos verificar a categoria do nadador
if ((idade >= 5) and (idade <= 7)):
print("Sua categoria é Infantil")
elif ((idade >= 8) and (idade <= 10)):
print("Sua categoria é Juvenil")
elif ((idade >= 11) and (idade <= 15)):
print("Sua categoria é Adolescente")
elif ((idade >= 16) and (idade <= 30)):
print("Sua categoria é Adulto")
elif (idade > 30):
print("Sua categoria é Sênior")
else:
print("Não pertence a nenhuma categoria.")
|
Python ::: Dicas & Truques ::: Lista (List) |
Python para iniciantes - Como usar o tipo de dados list da linguagem PythonQuantidade de visualizações: 7779 vezes |
|
O tipo de dados list é um dos quatro tipos de dados já incluídos no Python (sem a necessidade de importar outros módulos), a saber, tuple, set e dict (dictionary), cada um com qualidades e uso diferentes. Uma list é uma sequência mutável e ordenada de itens. Os itens de uma list são objetos arbitrários e podem ser de diferentes tipos. Para especificar uma list, podemos usar uma série de expressões (os itens da lista) separadas por vírgulas e entre colchetes ([]). Opcionalmente podemos inserir uma vírgula redundante depois do último item. Para denotar uma lista vazia, use um par de colchetes. Veja alguns exemplos: ---------------------------------------------------------------------- Se precisar de ajuda para ajustar o código abaixo de acordo com as suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar) Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar a manter o site livre de anúncios. Ficaremos eternamente gratos ;-) Nosso PIX é: osmar@arquivodecodigos.com.br ---------------------------------------------------------------------- # uma list com nomes de pessoas nomes = ['Carlos', 'Fabiana', 'Jorge'] print(nomes[0]) # uma list com valores inteiros valores = [3, 7, 34, 0, 2] print((valores[1] + valores[4])) # uma lista vazia lista = [] print(len(lista)) É possível também construir uma lista usando a palavra-chave list. Veja: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# função principal do programa
def main():
# uma list com nomes de pessoas
nomes = list(['Carlos', 'Fabiana', 'Jorge'])
print("O nome escolhido é", nomes[0])
if __name__== "__main__":
main()
Ao executar este último exemplo nós teremos o seguinte resultado: O nome escolhido é Carlos |
Python ::: Python para Engenharia ::: Engenharia Civil - Cálculo Estrutural |
Como calcular o Índice de Esbeltez de um pilar em Python - Python para Engenharia Civil e Cálculo EstruturalQuantidade de visualizações: 240 vezes |
 O índice de esbeltez de um pilar, representado pela letra grega λ (lambda) é uma relação que mede a altura do pilar em relação à sua largura ou seção transversal. Esse índice é usado para avaliar a suscetibilidade de um pilar à flambagem, que é um tipo de falha estrutural que pode ocorrer em pilares esbeltos sob compressão. Segundo a NBR 6118, 15.8.2, os pilares devem ter índice de esbeltez menor ou igual a 200 (λ ≤ 200). Apenas no caso de postes com força normal menor que 0,10 fcd x Ac, o índice de esbeltez pode ser maior que 200. O índice de esbeltez é a razão entre o comprimento de flambagem e o raio de giração, nas direções a serem consideradas. De acordo com o comprimento de flambagem, os pilares classificam-se como: curto, se λ < 35; medianamente esbelto, se 35 < λ < 90; esbelto, se 90 < λ < 140; e muito esbelto, se 140 < λ < 200. A fórmula para o cálculo do índice de esbeltez pode ser definida como: \[\lambda = 3,46 \cdot \frac{le}{h} \] Onde: λ = número adimensional representando o índice de esbeltez ao longo da direção escolhida (x ou y); le = algura do pilar, ou seja, o comprimento do pilar em centímetros. h = dimensão escolhida (x ou y) em centímetros. De acordo com a norma NBR 6118 (ABNT, 2014), se o índice de esbeltez na direção escolhida for menor que 35, nós não precisamos considerar os efeitos locais de 2ª ordem. Vamos agora ao código Python? Pediremos ao usuário para informar o comprimento (altura) do pilar em metros, as dimensões nas direções x e y e mostraremos os índices de esbeltez nas direções x e y do pilar com as respectivas anotações da necessidade ou não da consideração dos efeitos locais de 2ª ordem. Veja: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# método principal
def main():
# vamos pedir o comprimento do pilar em metros (pé direito)
le = float(input("Informe o comprimento do pilar (em metros): "))
# vamos converter o comprimento em metros para centímetros
le = le * 100.0
# vamos pedir as dimensões do pilar
hx = float(input("Informe a dimensão do pilar na direção x (em cm): "))
hy = float(input("Informe a dimensão do pilar na direção y (em cm): "))
# agora vamos calcular o índice de esbeltez na direção x
lambda_x = 3.46 * (le / hx)
# agora vamos calcular o índice de esbeltez na direção y
lambda_y = 3.46 * (le / hy)
# e mostramos os resultados
print("\nO índice de esbeltez na direção x é: {0}".format(round(lambda_x, 2)))
# precisamos considerar os efeitos locais de segunda ordem na direção x?
if lambda_x < 35:
print("Não considerar os efeitos locais de 2ª ordem na direção x")
else:
print("Considerar os efeitos locais de 2º ordem na direção x")
print("\nO índice de esbeltez na direção y é: {0}".format(round(lambda_y, 2)))
# precisamos considerar os efeitos locais de segunda ordem na direção y?
if lambda_y < 35:
print("Não considerar os efeitos locais de 2ª ordem na direção y")
else:
print("Considerar os efeitos locais de 2ª ordem na direção y")
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Informe o comprimento do pilar (em metros): 2.88 Informe a dimensão do pilar na direção x (em cm): 40 Informe a dimensão do pilar na direção y (em cm): 19 O índice de esbeltez na direção x é: 24.91 Não considerar os efeitos locais de 2ª ordem na direção x O índice de esbeltez na direção y é: 52.45 Considerar os efeitos locais de 2ª ordem na direção y |
Python ::: Python para Engenharia ::: Geometria Analítica e Álgebra Linear |
Python para Engenharia - Como multiplicar um vetor por um escalar usando Python e NumPyQuantidade de visualizações: 3379 vezes |
|
Esta dica de Python e NumPy é direcionada, principalmente, aos estudantes de Engenharia, que se deparam, logo no início do curso, com o estudo da Geometria Analítica e gostariam de entender melhor a multiplicação de vetores por um escalar. Lembre-se de que um escalar é um valor único, enquanto vetores e matrizes são estruturas que guardam vários valores ao mesmo tempo. Nosso primeiro exemplo será feito em cima de um vetor no R3, ou seja, no espaço, com os seguintes valores: [3, -5, 4]. O escalar usado será o valor 2, ou seja, temos que multiplicar cada valor no vetor pelo valor 2 e, dessa forma, obtermos um novo vetor, também no R3. Vetores no R3 possuem valores para x, y e z (três dimensões), enquanto vetores no R2 possuem apenas o x e y. Veja como a linguagem Python facilita a operação da multiplicação de um vetor R3 por um escalar: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# importamos a bibliteca NumPy
import numpy as np
def main():
# declara e cria o vetor
vetor = np.array([3, -5, 4])
# agora vamos multiplicar este vetor pelo escalar 2
escalar = 2
novoVetor = vetor * escalar
# vamos exibir o resultado
print("Vetor inicial: ", vetor)
print("Valor do escalar: ", escalar)
print("Novo vetor: ", novoVetor)
if __name__== "__main__":
main()
Este código Python vai gerar o seguinte resultado: Vetor inicial: [3 -5 4] Valor do escalar: 2 Novo vetor: [6 -10 8] Agora, saindo da Geometria Analítica e indo para a Álgebra Linear, veja como podemos efetuar a mesma operação em uma matriz de 2 linhas e 3 colunas (recorde que, em Python, uma matriz nada mais é do que um vetor de vetores, ou seja, cada elemento do vetor contém outro vetor): ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# importamos a bibliteca NumPy
import numpy as np
def main():
# declara e cria a matriz
matriz = np.array([(4, 12, 50), (5, 3, 1), (11, 9, 7)])
# agora vamos multiplicar esta matriz pelo escalar 2
escalar = 2
novaMatriz = matriz * escalar
# vamos exibir o resultado
print("Matriz inicial: ", matriz)
print("Valor do escalar: ", escalar)
print("Nova matriz: ", novaMatriz)
if __name__== "__main__":
main()
Ao executarmos este código Python nós teremos o seguinte resultado: Matriz inicial: [[4 12 50] [5 3 1] [11 9 7]] Valor do escalar: 2 Nova matriz: [[8 24 100] [10 6 2] [22 18 14]] |
Vamos testar seus conhecimentos em Python |
Qual o resultado da execução do seguinte código Python?# função usada para trocar dois itens de posição em uma lista def trocar_posicao(lista, pos1, pos2): lista[pos1], lista[pos2] = lista[pos2], lista[pos1] return lista # cria uma lista valores = [1, 2, 3, 4] # define as posições de troca pos1, pos2 = 0, 3 # chama a função de troca e retorna a nova lista print(trocar_posicao(valores, pos1, pos2)) A) [1, 4, 3, 2] B) [3, 2, 4, 1] C) [4, 2, 3, 1] D) [4, 4, 3, 2] E) [4, 3, 2, 1] Verificar Resposta Estudar Cards Todas as Questões |
Vamos testar seus conhecimentos em Python |
Qual o resultado da execução do seguinte código Python?
valor = 76.1234
print("O valor é: %0.2f" % valor)
A) O valor é: 76.00 B) O valor é: 76.12 C) O valor é: 0076 D) O valor é: 0.76 E) O valor é: 76.13 Verificar Resposta Estudar Cards Todas as Questões |
Vamos testar seus conhecimentos em Python |
| Qual função é usada para converter uma string em letras maiúsculas em Python? A) toUpper() B) upper() C) upper_case() D) toUpperCase() E) uppercase() Verificar Resposta Estudar Cards Todas as Questões |
Vamos testar seus conhecimentos em |
| Madeiras Com o avanço tecnológico, a construção civil tem se beneficiado significativamente com o desenvolvimento de diversos tipos de madeiras que oferecem soluções cada vez mais eficientes e sustentáveis. Essa evolução permitiu a criação de materiais que atendem às demandas específicas dos projetos, garantindo alta resistência, durabilidade e versatilidade. Em relação aos tipos de madeiras, considere V para verdadeiro e F para falso: ( ) A madeira serrada é o produto resultante do corte longitudinal de toras ou toretes de árvores por uma serra. ( ) A madeira reconstituída é composta por várias camadas finas de madeira sobrepostas e coladas em direções alternadas. ( ) A madeira compensada é produzida a partir do processamento da madeira natural em fibras, partículas ou lâminas, que são, então, reunidas e prensadas. Assinale a alternativa que apresenta a sequência correta. A) F, F e F. B) F, F e V. C) F, V e V. D) V, F e F. E) V, V e F. Verificar Resposta Estudar Cards Todas as Questões |
Vamos testar seus conhecimentos em |
| Vidros O vidro: A) É um material homogêneo. B) Orgânico. C) Formada pela fusão de uma massa resfriada. D) Quanto mais rápido for resfriado maior será sua densidade. E) É um material cristalino. Verificar Resposta Estudar Cards Todas as Questões |
Desafios, Exercícios e Algoritmos Resolvidos de Python |
Veja mais Dicas e truques de Python |
Dicas e truques de outras linguagens |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |
