Osmar J. Silva

Ofereço ajuda em Java, C/C++, Python, C#, LISP, AutoLisp, AutoCAD

+55 (062) 98553-6711

José de Angelis

Ofereço ajuda em PHP, Python, C#, JavaScript, Laravel, Google Ads e SEO

+55 (062) 98243-1195

	E-Book 350 Exercícios Resolvidos de Java - PDF com 500 páginas
	Domine lógica de programação e a linguagem Java com o nosso E-Book 350 Exercícios Exercícios de Java, para você estudar onde e quando quiser. Este e-book contém exercícios resolvidos abrangendo os tópicos: Java básico, matemática e estatística, programação dinâmica, strings e caracteres, entrada e saída, estruturas condicionais, vetores e matrizes, funções, laços, recursividade, internet, arquivos e diretórios, programação orientada a objetos e muito mais.
	Ver Conteúdo do E-book Apenas R$ 19,90

Você está aqui: C ::: C para Engenharia ::: Geometria Analítica e Álgebra Linear

Como calcular o determinante de uma matriz 3x3 usando a Regra de Sarrus em C - Linguagem C para Álgebra Linear

Quantidade de visualizações: 4978 vezes

Os estudos da Geometria Analítica e Álgebra Linear envolvem, em boa parte de seus cálculos, a magnitude de vetores, ou seja, o módulo, tamanho, comprimento ou intensidade dos vetores. E isso não é diferente em relação às matrizes.

Quando uma matriz é envolvida nos cálculos, com muita frequência precisamos obter o seu determinante, que nada mais é que um número real associado à todas as matrizes quadradas.

Nesta dica mostrarei como obter o determinante de uma matriz quadrada de ordem 3, ou seja, três linhas e três colunas, usando a regra de Sarrus (somente matrizes 3x3). Note que é possível obter o mesmo resultado com o Teorema de Laplace, que não está restrito às matrizes quadradas de ordem 3. Veja também que não considerei as propriedades do determinante, o que, em alguns casos, simplifica muito os cálculos.

Então, vamos supor a seguinte matriz 3x3: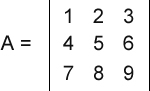

O primeiro passo é copiarmos a primeira e a segunda colunas para o lado direito da matriz. Assim: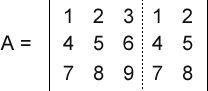

Agora dividimos a matriz em dois conjuntos: três linhas diagonais descendentes e três linhas diagonais ascendentes: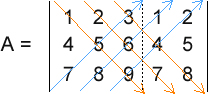

Agora é só efetuar cálculos. Multiplicamos e somamos os elementos de cada conjunto, subtraindo o segundo conjunto do primeiro. Veja:

(1 x 5 x 9 + 2 x 6 x 7 + 3 x 4 x 8) - (7 x 5 x 3 + 8 x 6 x 1 + 9 x 4 x 2) = 0

Como podemos ver, o determinante dessa matriz é 0.

E agora veja o código C no qual declaramos e instanciamos uma matriz 3x3 de double e, em seguida, calculamos o seu determinante:

----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
 
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br 
----------------------------------------------------------------------
 
#include <stdio.h>
#include <stdlib.h>
  
int main(int argc, char *argv[]){
  // vamos declarar e inicializar uma matriz 3x3
  double m[3][3] = {{1, 2, 3}, {2, 5, 2}, {1, 3, 1}};
     
  // calcula o determinante usando a Regra de Sarrus
  double det = ((m[0][0] * m[1][1] * m[2][2]) + (m[0][1] 
    * m[1][2] * m[2][0]) + (m[0][2] * m[1][0] * m[2][1])) 
    - ((m[2][0] * m[1][1] * m[0][2]) + (m[2][1] 
    * m[1][2] * m[0][0]) + (m[2][2] * m[1][0] * m[0][1]));
     
  // vamos mostrar o determinante
  printf("O determinante da matriz é %f", det);
   
  printf("\n\n");
  system("PAUSE");
  return 0;
}

Ao executar este código C nós teremos o seguinte resultado:

O determinante da matriz é: 2.0

Link para compartilhar na Internet ou com seus amigos:

Desafios, Exercícios e Algoritmos Resolvidos de C

Uma locadora de charretes cobra R$ 10,00 de taxa para cada 3 horas de uso destas - Exercício Resolvido de C

A loja ELETROMÓVEIS está vendendo os seus produtos no cartão em 5 vezes sem juros. Faça um algoritmo C que - Exercícios Resolvidos de C

Dado um número inteiro positivo n, se n for par, seu código deverá dividí-lo por 2, e - Exercício Resolvido de C

Escreva um programa C que pede para o usuário informar um número inteiro positivo de dois dígitos (Ex: 17) e mostre a soma de seus dígitos - Exercícios Resolvidos de C

Como converter quilômetros em metros, centímetros e milímetros usando C - Exercício Resolvido de C

A empresa GÁS TOTAL paga uma gratificação de R$ 237,50 a todos os seus funcionários. Escreva um programa C - Exercícios Resolvidos de C

Como desenhar um triângulo de números em C usando laços - Exercícios Resolvidos de C

Como calcular o peso de uma pessoa na Lua usando C - Exercício Resolvido de C

Ler um número inteiro na faixa 0-999 e mostrar a soma de seus dígitos - C Básico - Exercícios Resolvidos de C

Como calcular os fatores de um número em C - C para Matemática - Exercícios Resolvidos de C

Programa de cálculo de médias de alunos. Escrever um programa C que cadastre o nome, a matrícula e duas notas de vários alunos - Exercício Resolvido de C

Escreva um programa em C que lê N números inteiros e os armazena em um vetor. O usuário deverá informar o tamanho do vetor (um número positivo entre 1 e 100) - Exercício Resolvido de C

Escreva um método recursivo em C que, dados dois inteiros a e b (a <= b), retorna a multiplicação dessa faixa de números - Exercício Resolvido de C

Escreva uma função C que recebe um vetor de inteiros e informe se os elementos do array estão classificados em ordem crescente - Exercícios Resolvidos de C

Declarar um vetor de 10 elementos e usar o laço for para solicitar ao usuário que informe os valores dos elementos do vetor - Exercício Resolvido de C

Exercícios Resolvidos de Física usando C - Aplica-se uma força de 20 N a um corpo de massa m. O corpo desloca-se em linha reta com velocidade que aumenta - Exercícios Resolvidos de C

Como testar se um retângulo cabe dentro de um círculo usando C - Exercício Resolvido de C

Ler três números inteiros e indicar se eles estão em ordem crescente ou decrescente - Exercícios Resolvidos de C

Na usina nuclear de Angra dos Reis, os técnicos analisam a perda de massa de um material radioativo. Sabendo-se que este - Exercícios Resolvidos de C

Escreva um programa em C para ler, calcular e escrever a média aritmética entre dois números - Exercício Resolvido de C

Escreva um programa em C que declara um vetor de 5 elementos do tipo int. Em seguida peça para o usuário informar os valores dos elementos - Exercícios Resolvidos de C

Escreva um programa em C para ler dois números inteiros M e N e, a seguir, imprimir os números pares - Exercício Resolvido de C

Um programa que lê três números inteiros e mostra o maior - Exercício Resolvido de C

Como resolver problemas de razão e proporção em C - Em uma empresa, a razão entre o número de mulheres e o número - Exercício Resolvido de C

Ler a idade e o peso de 10 pessoas e mostrar a quantidade de pessoas com mais de 80 quilos e a média das idades - Exercícios Resolvidos de C

Como escrever uma função C que recebe dois números inteiros e retorna a soma desses dois valores como um inteiro - Exercício Resolvido de C

Um comerciante comprou um produto e quer vendê-lo com um lucro de 45% se o valor da compra for menor - Exercício Resolvido de C

Fazer um programa para receber um número inteiro de segundos do usuário e imprimir a quantidade correspondente em horas - Exercícios Resolvidos de C

Escreva um programa C para ler uma data no formato DD/MM/YYYY e informar se a data é válida ou não, considerando o caso do ano bissexto - Exercício Resolvido de C

Desenvolva um programa que calcule a média das notas de alunos para uma turma de no máximo 100 alunos - Exercícios Resolvidos de C

Veja mais Dicas e truques de C

Apostila C para iniciantes - Como converter de binário para decimal usando a linguagem C

C para iniciantes - Como ordenar os elementos de um vetor de inteiros usando a ordenação da bolha (Bubble Sort) na linguagem C

Como obter a quantidade de elementos em uma matriz C

Exercícios Resolvidos de C - Como retornar o código ASCII associado a um caractere em C - Ler um caractere e retornar o código ASCII correspondente

Ordenação e pesquisa em C - Como ordenar um vetor de inteiros usando a ordenação Insertion Sort (Ordenação por Inserção)

Como calcular o ponto de interseção de duas retas em C - C para Geometria Analítica e Álgebra Linear

Como calcular a área do trapézio em C - C para Geometria Plana

Como escrever uma função recursiva para calcular a potência de um número usando a linguagem C

Como elevar uma base a um determinado expoente usando a função pow() da linguagem C

Exercícios Resolvidos de C - Como contar as linhas de um arquivo usando C

Dicas e truques de outras linguagens

Ruby - Como testar se uma string começa com uma determinada substring em Ruby usando uma função personalizada

Delphi - Como carregar uma imagem JPG, convertê-la em Bitmap e desenhá-la no formulário usando Delphi

Python - Como usar o método read_csv() do Pandas da linguagem Python para carregar um dataset e retorná-lo como um DataFrame

PHP - PHP para iniciantes - Como usar o tipo de dados float do PHP

Dart - Como usar o laço while da linguagem Dart

C++ - Como renomear arquivos e diretórios em C++ usando a função MoveFile() da API do Windows

C# - C# Windows Forms para iniciantes - Como limpar todo o conteúdo de um controle TextBox via código

Python - Como converter uma string para um valor numérico inteiro usando a função int() do Python

C# - Como pesquisar e retornar o índice de um item na ListBox do C# Windows Forms

jQuery - Apostila jQuery - Como definir propriedades style CSS de elementos HTML usando a função css() do jQuery

E-Books em PDF

E-Book 650 Dicas, Truques e Exercícios Resolvidos de Python - PDF com 1.200 páginas

Domine lógica de programação e a linguagem Python com o nosso E-Book 650 Dicas, Truques e Exercícios Exercícios de Python, para você estudar onde e quando quiser.

Este e-book contém dicas, truques e exercícios resolvidos abrangendo os tópicos: Python básico, matemática e estatística, banco de dados, programação dinâmica, strings e caracteres, entrada e saída, estruturas condicionais, vetores e matrizes, funções, laços, recursividade, internet, arquivos e diretórios, programação orientada a objetos e muito mais.

Ver Conteúdo do E-book

E-Book 350 Exercícios Resolvidos de Java - PDF com 500 páginas

Domine lógica de programação e a linguagem Java com o nosso E-Book 350 Exercícios Exercícios de Java, para você estudar onde e quando quiser.

Este e-book contém exercícios resolvidos abrangendo os tópicos: Java básico, matemática e estatística, programação dinâmica, strings e caracteres, entrada e saída, estruturas condicionais, vetores e matrizes, funções, laços, recursividade, internet, arquivos e diretórios, programação orientada a objetos e muito mais.

Ver Conteúdo do E-book

Linguagens Mais Populares

1º lugar: Java
2º lugar: Python
3º lugar: C#
4º lugar: PHP
5º lugar: C
6º lugar: Delphi
7º lugar: JavaScript
8º lugar: C++
9º lugar: VB.NET
10º lugar: Ruby

Você está aqui: C ::: C para Engenharia ::: Geometria Analítica e Álgebra Linear

Como calcular o determinante de uma matriz 3x3 usando a Regra de Sarrus em C - Linguagem C para Álgebra Linear

Questões de Concurso para Engenharia Civil

Exercícios Resolvidos

Bancos de Dados

Questões de Concurso

Frameworks

Projetos e Códigos Fonte

Especializações

Calculadoras

Ferramentas

Todas as Linguagens, Frameworks, Biliotecas e Bancos de Dados

Compre pelo WhatsApp: +55 (062) 98553-6711

E-Book 650 Dicas, Truques e Exercícios Resolvidos de Python - Com comentários em Português

PDF COM 1.200 PÁGINAS

Apenas R$ 32,90