 |
|
||||
 Código-Fonte Software de Gestão Financeira com código fonte em PHP, MySQL, Bootstrap, jQuery - Inclui cadastro de clientes, fornecedores e ticket de atendimentoDiga adeus às planilhas do Excel e tenha 100% de controle sobre suas contas a pagar e a receber, gestão de receitas e despesas, cadastro de clientes e fornecedores com fotos e histórico de atendimentos. Código fonte completo e funcional, com instruções para instalação e configuração do banco de dados MySQL. Fácil de modificar e adicionar novas funcionalidades. Clique aqui e saiba mais |
|||||
Você está aqui: GNU Octave ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
|
Como calcular o seno de um número ou ângulo em GNU Octave usando a função sin()Quantidade de visualizações: 2639 vezes |
|
|
Em geral, quando falamos de seno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função seno disponível nas linguagens de programação para calcular o seno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função seno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o seno é a razão entre o cateto oposto (oposto ao ângulo theta) e a hipotenusa, ou seja, o cateto oposto dividido pela hipotenusa. Veja a fórmula: \[\text{Seno} = \frac{\text{Cateto oposto}}{\text{Hipotenusa}} \] Então, se dividirmos 20 por 36.056 (na figura eu arredondei) nós teremos 0.5547, que é a razão entre o cateto oposto e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.5547. O resultado será 0.9828 (em radianos). Convertendo 0.9828 radianos para graus, nós obtemos 56.31º, que é exatamente o ângulo em graus entre o cateto oposto e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é seno na trigonometria, vamos entender mais sobre a função sin() da linguagem GNU Octave. Esta função, que já vem embutido na ferramenta, recebe um valor numérico e retorna um valor, também numérico) entre -1 até 1 (ambos inclusos). Veja:
Note que calculamos os senos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função seno mostrada abaixo:  |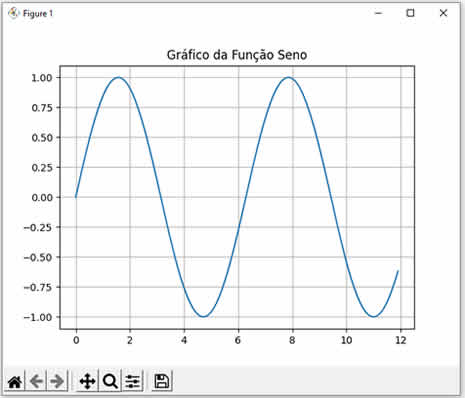
|
 Link para compartilhar na Internet ou com seus amigos: |
|
Veja mais Dicas e truques de GNU Octave |
Dicas e truques de outras linguagens |
|
C++ - Programação Orientada a Objetos em C++ - Como criar e usar métodos estáticos em suas classes C++ |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |
