Você está aqui: Python ::: Matplotlib Python Library (Biblioteca Python Matplotlib) ::: Geração e Plotagem de Gráficos usando Matplotlib |
Como gerar o gráfico da função cosseno usando a biblioteca Matplotlib do PythonQuantidade de visualizações: 2681 vezes |
|
A função cosseno (ou coseno) é a razão entre o cateto adjacente e a hipotenusa de um triângulo retângulo, ou seja, trata-se de uma razão trigonométrica que retorna valores na faixa de -1 até 1 (ambos inclusos). Nesta dica mostrarei como podemos usar as capacidades de geração de gráficos da biblioteca Matplotlib da linguagem Python, combinadas com as funções arange() e cos() da biblioteca NumPy para gerar o gráfico da função cosseno. Antes de vermos o código, observe o resultado gerado na imagem a seguir: 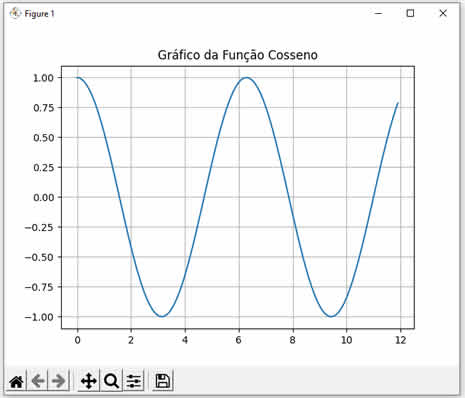 Veja agora o código Python completo para a geração do gráfico:
# importamos a biblioteca NumPy
import numpy as np
#importamos a biblioteca Matplotlib
import matplotlib.pyplot as plt
def main():
# definimos o título para a área de plotagem
plt.title('Gráfico da Função Cosseno')
# vamos exibir o grid da área de plotagem
plt.grid(True)
# vamos definir os valores da coordenada x
# os valores gerados serão de 0 até 12 (não incluso)
eixo_x = np.arange(0, 12, 0.1)
|
|
|
Desafios, Exercícios e Algoritmos Resolvidos de Python |
Veja mais Dicas e truques de Python |
Dicas e truques de outras linguagens |
|
GNU Octave - Como calcular o coeficiente angular de uma reta em GNU Octave dados dois pontos no plano cartesiano |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |






