 |
|
||||
Você está aqui: Python ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Geometria com Python - Como calcular o ponto médio entre dois pontos no plano usando PythonQuantidade de visualizações: 4447 vezes |
|
Nesta dica mostrarei como é possível usar um trecho de código Python para obter o ponto médio entre dois pontos quaisquer no plano, ou seja, no R2. Em mais dicas dessa seção você aprenderá como isso pode ser feito no R3 (espaço) Comece analisando a figura abaixo, na qual temos dois pontos A e B, com suas coordenadas correspondentes, e o ponto médio M: 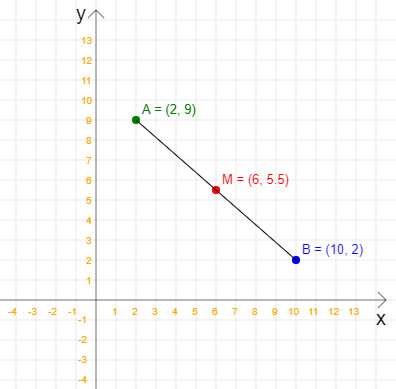 Assim, dados dois pontos A = (2, 9) e B = (10, 2) no plano cartesiano R2, as coordenadas x e y do ponto médio são calculadas por meio da seguinte fórmula: \[x = \frac{x_1 + x_2}{2}\] \[y = \frac{y_1 + y_2}{2}\] Colocando na fórmula os valores que já temos: \[x = \frac{2 + 10}{2} = \frac{12}{2} = 6 \] \[y = \frac{9 + 2}{2} = \frac{11}{2} = 5.5 \] Assim, as coordenadas do ponto médio será (x = 6, y = 5.5). E agora veja o código Python completo para calcular as coordenadas do ponto médio a partir de dois pontos no plano cartesiano (plano 2D ou R2): ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
import math
# função que permite calcular a distância
# entre dois pontos no plano (R2)
def distancia2d(x1, y1, x2, y2):
a = x2 - x1
b = y2 - y1
c = math.sqrt(math.pow(a, 2) + math.pow(b, 2))
return c
# função principal do programa
def main():
# vamos ler os dados do primeiro ponto
x1 = float(input("Informe o x do primeiro ponto: "))
y1 = float(input("Informe o y do primeiro ponto: "))
# vamos ler os dados do segundo ponto
x2 = float(input("Informe o x do segundo ponto: "))
y2 = float(input("Informe o y do segundo ponto: "))
# vamos calcular as coordenadas x e y do ponto médio
x = (x1 + x2) / 2
y = (y1 + y2) / 2
# vamos mostrar o resultado
print("As coordenadas do ponto médio são: (x = %0.1f, y = %0.1f)"
% (x, y))
if __name__== "__main__":
main()
Ao executarmos este código Python nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 2 Coordenada y do primeiro ponto: 9 Coordenada x do segundo ponto: 10 Coordenada y do segundo ponto: 2 As coordenadas do ponto médio são: (x = 6.0, y = 5.5) |
 Link para compartilhar na Internet ou com seus amigos: |
Python ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o seno de um número ou ângulo em Python usando a função sin() do módulo MathQuantidade de visualizações: 1327 vezes |
|
Em geral, quando falamos de seno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função seno disponível nas linguagens de programação para calcular o seno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função seno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o seno é a razão entre o cateto oposto (oposto ao ângulo theta) e a hipotenusa, ou seja, o cateto oposto dividido pela hipotenusa. Veja a fórmula: \[\text{Seno} = \frac{\text{Cateto oposto}}{\text{Hipotenusa}} \] Então, se dividirmos 20 por 36.056 (na figura eu arredondei) nós teremos 0.5547, que é a razão entre o cateto oposto e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.5547. O resultado será 0.9828 (em radianos). Convertendo 0.9828 radianos para graus, nós obtemos 56.31º, que é exatamente o ângulo em graus entre o cateto oposto e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é seno na trigonometria, vamos entender mais sobre a função sin() da linguagem Python. Este método, que faz parte do módulo Math, recebe um valor numérico e retorna um valor, também numérico) entre -1 até 1 (ambos inclusos). Veja: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# importamos a biblioteca Math
import math as math
def main():
print("Seno de 0 = ", math.sin(0))
print("Seno de 1 = ", math.sin(1))
print("Seno de 2 = ", math.sin(2))
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Seno de 0 = 0.0 Seno de 1 = 0.8414709848078965 Seno de 2 = 0.9092974268256817 Note que calculamos os senos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função seno mostrada abaixo:  |
Python ::: Dicas & Truques ::: Data e Hora |
Datas e horas em Python - Como obter a hora como um decimal no intervalo 00-12 (formato 12 horas)Quantidade de visualizações: 7423 vezes |
|
Este exemplo mostra como obter a hora como um decimal no intervalo 00-12 (formato 12 horas) usando o método strftime() da classe datetime com o sinalizador "%I". Veja o código completo para a dica: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
from datetime import datetime
def main():
# Obtém um datetime da data e hora atual
hoje = datetime.today()
# Exibe a hora atual como um decimal
print(hoje.strftime("A hora é: %I"))
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: A hora é: 10 |
Python ::: wxPython ::: wxFrame |
Como definir o ícone para uma janela wx.Frame do wxPythonQuantidade de visualizações: 7282 vezes |
|
Nesta dica mostrarei como usar a função SetIcon() da classe wx.TopLevelWindow para definir o ícone da janela de nossa aplicação wxPython. Observe que, se o ícone não for encontrado, uma mensagem de erro será exibida. Veja o código completo para o exemplo: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# vamos importar a biblioteca Wx
import wx
# vamos criar uma classe que herda de wxFrame
class MinhaJanela(wx.Frame):
def __init__(self):
# chamamos o construtor da super classe
wx.Frame.__init__(self, None, -1,
"Cadastro de Clientes", size=(350, 200))
# Define o ícone para a janela
self.SetIcon(wx.Icon("icone.ico", wx.BITMAP_TYPE_ICO))
if __name__ == "__main__":
app = wx.App()
janela = MinhaJanela()
janela.Show(True)
app.MainLoop()
|
Python ::: Dicas & Truques ::: Arquivos e Diretórios |
Como criar um diretório em Python usando a função mkdir() do módulo osQuantidade de visualizações: 3126 vezes |
|
Podemos usar a função mkdir() do módulo os da linguagem Python para criarmos diretórios. Em sua versão mais simples, este método pede somente o nome e caminho do diretório a ser criado. Se o caminho for omitido, o novo diretório será criado no diretório atual, ou seja, o diretório da aplicação Python. Veja um exemplo no qual criamos um diretório chamado "app" no diretório "C:\estudos_python": ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# importa o módulo os
import os
# método principal
def main():
# nome do diretório
diretorio = "C:\\estudos_python\\app"
# vamos criar o diretório
os.mkdir(diretorio)
# mostramos o resultado
print('O diretório foi criado com sucesso.')
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: c:\estudos_python>python estudos.py O diretório foi criado com sucesso. Note que um erro do tipo FileExistsError será exibido se o diretório já existir: Traceback (most recent call last): File "c:\estudos_python\estudos.py", line 16, in <module> main() File "c:\estudos_python\estudos.py", line 10, in main os.mkdir(diretorio) FileExistsError: [WinError 183] Não é possível criar um arquivo já existente: 'C:\\estudos_python\\app' Uma forma de evitar este erro é verificar se o diretório já existe ou usar uma construção try...except. Veja: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# importa o módulo os
import os
# método principal
def main():
# nome do diretório
diretorio = "C:\\estudos_python\\app"
try:
# vamos criar o diretório
os.mkdir(diretorio)
# mostramos o resultado
print('O diretório foi criado com sucesso.')
except os.error as error_msg:
print("Houve um erro: %s" % str(error_msg))
if __name__== "__main__":
main()
Execute o código novamente e veja como o tratamento de erro ficou mais elegante. |
Python ::: Dicas & Truques ::: Data e Hora |
Como adicionar dias à uma data em Python usando a função timedelta() da classe datetimeQuantidade de visualizações: 8971 vezes |
|
Nesta dica mostrarei como é possível usar o método timedelta() da classe datetime do Python para adicionar um determinado número de dias a uma data. O truque aqui é fornecer apenas o dia para o método timedelta(), obter o resultado e somá-lo com a data que já temos. Veja o código completo para o exemplo: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
import datetime
# função principal do programa
def main():
# dias a serem adicionados
quant_dias = 2
# Obtém a data de hoje
hoje = datetime.date.today()
print("Hoje é:", hoje)
# Adiciona dias à data
dias = datetime.timedelta(days=quant_dias)
hoje = hoje + dias
# Exibe o resultado
print("Daqui à", quant_dias, "dias será", hoje)
if __name__== "__main__":
main()
Ao executarmos este código Python nós teremos o seguinte resultado: Hoje é: 2021-03-11 Daqui à 2 dias será 2021-03-13 |
Python ::: Python para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como calcular a norma ou módulo de vetores nos espaços R2 e R3 usando Python - Geometria Analítica e Álgebra Linear usando PythonQuantidade de visualizações: 3783 vezes |
|
Em Geometria Analítica e Álgebra Linear, a magnitude, norma, comprimento, tamanho ou módulo (também chamado de intensidade na Física) de um vetor é o seu comprimento, que pode ser calculado por meio da distância de seu ponto final a partir da origem, no nosso caso (0,0). Considere o seguinte vetor no plano, ou seja, no espaço bidimensional, ou R2: \[\vec{v} = \left(7, 6\right)\] Aqui este vetor se inicia na origem (0, 0) e vai até as coordenadas (x = 7) e (y = 6). Veja sua plotagem no plano 2D:  Note que na imagem já temos todas as informações que precisamos, ou seja, o tamanho desse vetor é 9 (arredondado) e ele faz um ângulo de 41º (graus) com o eixo x positivo. Em linguagem mais adequada da trigonometria, podemos dizer que a medida do cateto oposto é 6, a medida do cateto adjacente é 7 e a medida da hipotenusa (que já calculei para você) é 9. Note que já mostrei também o ângulo theta (__$\theta__$) entre a hipotenusa e o cateto adjacente, o que nos dá a inclinação da reta representada pelos pontos (0, 0) e (7, 6). Relembrando nossas aulas de trigonometria nos tempos do colegial, temos que o quadrado da hipotenusa é a soma dos quadrados dos catetos, ou seja, o Teorema de Pitágoras: \[a^2 = b^2 + c^2\] Como sabemos que a potenciação é o inverso da radiciação, podemos escrever essa fórmula da seguinte maneira: \[a = \sqrt{b^2 + c^2}\] Passando para os valores x e y que já temos: \[a = \sqrt{7^2 + 6^2}\] Podemos comprovar que o resultado é 9,21 (que arredondei para 9). Não se esqueça da notação de módulo ao apresentar o resultado final: \[\left|\vec{v}\right| = \sqrt{7^2 + 6^2}\] E aqui está o código Python que nos permite informar os valores x e y do vetor e obter o seu comprimento, tamanho ou módulo: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# função principal do programa
def main():
# vamos ler os valores x e y
x = float(input("Informe o valor de x: "))
y = float(input("Informe o valor de y: "))
# vamos calcular a norma do vetor
norma = math.sqrt(math.pow(x, 2) + math.pow(y, 2))
# mostra o resultado
print("A norma do vetor é: %0.2f" % norma)
if __name__== "__main__":
main()
Ao executar este código nós teremos o seguinte resultado: Informe o valor de x: 7 Informe o valor de y: 6 A norma do vetor é: 9.22 Novamente note que arredondei o comprimento do vetor para melhor visualização no gráfico. Para calcular a norma de um vetor no espaço, ou seja, no R3, basta acrescentar o componente z no cálculo. |
Python ::: Dicas & Truques ::: Lista (List) |
Como inverter a ordem dos elementos em uma lista Python usando o método reverse()Quantidade de visualizações: 17045 vezes |
|
Inverter a ordem dos itens de um vetor ou lista é uma das tarefas mais corriqueiras durante o trabalho de programação. Na linguagem Python nós podemos inverter os elementos de uma list usando o método reverse(), já embutido na linguagem. Este método modifica a lista original. Veja um exemplo de seu uso: ---------------------------------------------------------------------- Se precisar de ajuda para ajustar o código abaixo de acordo com as suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar) Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar a manter o site livre de anúncios. Ficaremos eternamente gratos ;-) Nosso PIX é: osmar@arquivodecodigos.com.br ---------------------------------------------------------------------- def main(): # cria uma lista de inteiros valores = [2, 5, 12, 2, 3, 32, 18] # exibe a lista na ordem original print(valores) # inverte a lista valores.reverse() # exibe a lista na ordem invertida print(valores) if __name__== "__main__": main() Ao executar este código Python nós teremos o seguinte resultado: [2, 5, 12, 2, 3, 32, 18] [18, 32, 3, 2, 12, 5, 2] |
Python ::: NumPy Python Library (Biblioteca Python NumPy) ::: Números Aleatórios, Números Randômicos, Amostras Aleatórias, Amostras Randômicas |
Como gerar um número randômico em Python usando a função rand() do módulo random da NumPyQuantidade de visualizações: 645 vezes |
Em algumas situações nós precisamos gerar um número aleatório na faixa de 0 e 1 (não incluído). Para isso nós podemos usar a função rand() do módulo random da biblioteca NumPy do Python. Veja um exemplo:----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# importamos o módulo random da biblioteca NumPy
import numpy as np
# método principal
def main():
# vamos gerar um número decimal aleatório de 0 (incluído)
# à 1 (não incluído)
valor = np.random.rand()
print("O número sorteado foi: {0}".format(valor))
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: O número sorteado foi: 0.2037063569952866 Note que o número retornado pela função rand() é um float com uma precisão semelhante ao double em outras linguagens de programação. Veja agora uma modificação deste código para gerar 10 números aleatórios: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# importamos o módulo random da biblioteca NumPy
import numpy as np
# método principal
def main():
# vamos gerar 10 números decimais aleatórios de 0 (incluído)
# à 1 (não incluído)
for i in range(10):
valor = np.random.rand()
print("O número sorteado foi: {0}".format(valor))
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: O número sorteado foi: 0.57920714427429 O número sorteado foi: 0.06329414607318185 O número sorteado foi: 0.12184477988071851 O número sorteado foi: 0.5410663009618577 O número sorteado foi: 0.790229323250604 O número sorteado foi: 0.4733277307431061 O número sorteado foi: 0.7669969432159425 O número sorteado foi: 0.6934927410217504 O número sorteado foi: 0.13216036543343856 O número sorteado foi: 0.6958612722883786 |
Desafios, Exercícios e Algoritmos Resolvidos de Python |
Veja mais Dicas e truques de Python |
Dicas e truques de outras linguagens |
|
JavaScript - Como calcular o cateto oposto dadas as medidas da hipotenusa e do cateto adjascente em JavaScript |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |
