Você está aqui: Python ::: NumPy Python Library (Biblioteca Python NumPy) ::: Matemática e Estatística

Tutorial Machine Learning com Python - Como usar o método mean() da biblioteca NumPy para calcular média (ou média aritmética simples)

Quantidade de visualizações: 4114 vezes

Média aritmética (ou simplesmente média simples) é a soma de vários valores e dividido pelo total deles. Ou seja, o resultado dessa divisão equivale a um valor médio entre todos os valores.

Veja a seguinte figura: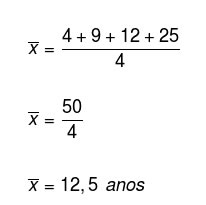

Veja que temos 4 valores: 4, 9, 12 e 25. Assim, para obter a média aritmética desses valores, só precisamos somá-los e depois dividir pela quantidade, ou seja, por 4. A média resultante será 12,5.

A biblioteca NumPy do Python nos oferece o método mean(), muito usado em Data Science e Machine Learning, que recebe um vetor de valores númericos (inteiro ou decimais) e retorna a média deles. Veja um exemplo:

----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------

# importamos a biblioteca NumPy
import numpy

def main():
  # valores a serem observados
  valores = [4, 9, 12, 25]

  # vamos obter a média aritmética simples
  media = numpy.mean(valores)

  # vamos mostrar o resultado
  print("A média dos valores é:", media)

if __name__== "__main__":
  main()

Ao executarmos este código nós teremos o seguinte resultado:

A média dos valores é: 12.5

Link para compartilhar na Internet ou com seus amigos:

Desafios, Exercícios e Algoritmos Resolvidos de Python

Exercícios Resolvidos de Física usando Python - Aplica-se uma força de 20 N a um corpo de massa m. O corpo desloca-se em linha reta com velocidade que aumenta - Exercício Resolvido de Python

Criar uma classe Veiculo com os atributos marca, modelo e cor. Peça para o usuário fornecer os valores dos atributos - Exercício Resolvido de Python

Usando um laço for para percorrer os elementos de um vetor e exibir a soma dos valores positivos e a quantidade de valores negativos - Exercícios Resolvidos de Python

Como calcular o ângulo entre os ponteiros de horas e minutos em um relógio analógico - Exercício Resolvido de Python

Como somar todos os números de 1 até o número informado pelo usuário em Python - Exercício Resolvido de Python

Python Básico - Escreva um programa que leia a quantidade de dias, horas, minutos e segundos do usuário. Calcule o total em segundos - Exercício Resolvido de Python

Uma força de intensidade 2N é aplicada perpendicularmente a uma superfície por meio de um pino de 1mm2 de área. Determine a pressão em N/m2 - Exercícios Resolvidos de Python

Exercício Resolvido de Python Pandas - Como converter uma List em uma Series do Pandas - Exercícios Resolvidos de Python

Como testar se um número é potência de dois usando Python - Exercício Resolvido de Python

Uma empresa de táxi cobra a bandeirada de R$ 5,00 e ainda o valor de R$ 1,50 para cada quilômetro rodado - Exercícios Resolvidos de Python

Escreva um programa em Python para o Ministério da Saúde que o auxilie nas informações sobre a dengue em Brasília. Esse programa - Exercícios Resolvidos de Python

Exercício Resolvido de Python NumPy - Como gerar uma matriz MxN no Python Numpy usando as funções arange() e reshape() - Exercícios Resolvidos de Python

Valor da diária, valor médio arrecadado com e sem promoção e o lucro ou prejuízo mensal de uma promoção em um hotel - Exercícios Resolvidos de Python

Um programa que lê a altura e o sexo de uma pessoa e informa seu peso ideal - Exercício Resolvido de Python

Como calcular salário líquido em Python - Calculando o salário líquido de um professor - Exercícios Resolvidos de Python

Como calcular o peso específico do solo em Python - Uma amostra cilíndrica de solo úmido foi moldada com 10 cm de diâmetro e 15 cm de altura - Exercícios Resolvidos de Python

Ler uma temperatura em graus Celsius e apresentá-la convertida em graus Fahrenheit - Exercícios Resolvidos de Python

Como criar um conversor de moedas em Python - Um programa Python para converter de Real para Dólar e de Dólar para Real - Exercício Resolvido de Python

Como converter decimal em binário em Python usando o laço while - Exercício Resolvido de Python

Uma barra de aço de 12,7 mm de diâmetro suporta uma carga de 7.000 kg. a) Qual é a tensão atuante na barra? b) Qual será a deformação? - Exercício Resolvido de Python

Como calcular o comprimento de um segmento de reta usando Python - Exercício Resolvido de Python

Escreva uma função Python que recebe três números inteiros e retorna o menor deles - Exercício Resolvido de Python

Programação Linear em Python - Uma madeireira deseja obter 1000kg de lenha, 2000kg de madeira para móveis e 50 metros - Exercício Resolvido de Python

Como calcular e exibir os 50 primeiros números primos em Python - Exercício Resolvido de Python

Como usar a Ordenação da Bolha em Python para ordenar os valores de um vetor em ordem crescente ou decrescente - Exercícios Resolvidos de Python

Como retornar o código ASCII associado a um caractere em Python - Ler um caractere e retornar o código ASCII correspondente - Exercícios Resolvidos de Python

Como testar se uma string Python contém somente os dígitos de 0 a 9 usando códigos ASCII - Exercícios Resolvidos de Python

Como multiplicar os dígitos de um número inteiro usando recursividade em Python - Exercícios Resolvidos de Python

Qual é o raio hidráulico em um canal de seção retangular com 2,00 m de largura por 1,20 m de altura? - Exercício Resolvido de Python

Como calcular o Número de Reynolds em Python - Um óleo é bombeado através de uma tubulação de 10 mm de diâmetro a um número de Reynolds de 2100 - Exercício Resolvido de Python

Veja mais Dicas e truques de Python

Como carregar um shapefile no GeoPandas e retornar o resultado como um GeoDataFrame

Exercícios Resolvidos de Python - Lendo a idade de um nadador e classificando sua categoria como infantil, juvenil, adolescente, adulto ou sênior

Como converter graus, minutos e segundos para graus decimais em Python

Como calcular a velocidade da queda livre de um corpo dado o intervalo de tempo (e a aceleração da gravidade) em Python

Python wxPython - Como criar janelas GUI em Python usando a classe wx.Frame do wxPython

Como definir o espaço interno do objeto Frame do Tkinter Python usando a propriedade padding

Como gerar permutações de uma string em Python usando o objeto permutations do módulo Itertools

Como adicionar novos itens a um dicionário Python

Cálculo de estribos em vigas de concreto armado usando Python - Armadura mínima transversal normativa

Como retornar o maior valor de uma Series do Pandas do Python usando a função max() do Numpy

Dicas e truques de outras linguagens

C - Exercícios Resolvidos de C - Escreva um programa C para mover todos os zeros para o final do vetor, sem alterar a ordem dos elementos já presentes no array

PHP - PHP para iniciantes - Como testar se uma variável é do tipo string usando a função is_string() do PHP

PHP - Como criar uma tabela MySQL usando o comando CREATE TABLE e as funções mysql_query() e mysqli_query() do PHP

R - Como calcular o coeficiente angular de uma reta em R dados dois pontos no plano cartesiano

JavaScript - Como retornar a diferença em dias entre duas datas usando JavaScript

Delphi - Como abrir e fechar um dispositivo de saída MIDI usando Delphi

Java - Java Swing - Como excluir linhas de uma JTable em tempo de execução usando o método removeRow() da classe DefaultTableModel

C# - Como somar os elementos da diagonal principal de uma matriz em C#

Java - Como testar se uma matriz é uma matriz identidade usando Java

C# - Como usar o controle DataGridView do C# Windows Forms

E-Books em PDF

E-Book 350 Exercícios Resolvidos de Java - PDF com 500 páginas

Domine lógica de programação e a linguagem Java com o nosso E-Book 350 Exercícios Exercícios de Java, para você estudar onde e quando quiser.

Este e-book contém exercícios resolvidos abrangendo os tópicos: Java básico, matemática e estatística, programação dinâmica, strings e caracteres, entrada e saída, estruturas condicionais, vetores e matrizes, funções, laços, recursividade, internet, arquivos e diretórios, programação orientada a objetos e muito mais.

Ver Conteúdo do E-book

E-Book 650 Dicas, Truques e Exercícios Resolvidos de Python - PDF com 1.200 páginas

Domine lógica de programação e a linguagem Python com o nosso E-Book 650 Dicas, Truques e Exercícios Exercícios de Python, para você estudar onde e quando quiser.

Este e-book contém dicas, truques e exercícios resolvidos abrangendo os tópicos: Python básico, matemática e estatística, banco de dados, programação dinâmica, strings e caracteres, entrada e saída, estruturas condicionais, vetores e matrizes, funções, laços, recursividade, internet, arquivos e diretórios, programação orientada a objetos e muito mais.

Ver Conteúdo do E-book

Linguagens Mais Populares

1º lugar: Java
2º lugar: Python
3º lugar: C#
4º lugar: PHP
5º lugar: C
6º lugar: Delphi
7º lugar: JavaScript
8º lugar: C++
9º lugar: VB.NET
10º lugar: Ruby

Você está aqui: Python ::: NumPy Python Library (Biblioteca Python NumPy) ::: Matemática e Estatística

Tutorial Machine Learning com Python - Como usar o método mean() da biblioteca NumPy para calcular média (ou média aritmética simples)

Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica.

Questões de Concurso para Engenharia Civil

Exercícios Resolvidos

Bancos de Dados

Questões de Concurso

Frameworks

Projetos e Códigos Fonte

Especializações

Calculadoras

Ferramentas

Todas as Linguagens, Frameworks, Biliotecas e Bancos de Dados

Compre pelo WhatsApp: +55 (062) 98553-6711

E-Book 350 Exercícios Resolvidos de Java - Com comentários em Português

PDF COM 500 PÁGINAS

Apenas R$ 19,90