Você está aqui: Python ::: wxPython ::: wxButton

Entenda e aprenda a usar a classe wx.Button

Quantidade de visualizações: 6927 vezes

Botões são os controles mais frequentes em interfaces do usuário (GUI) e o wxPython nos fornece a classe wx.Button, usada para criar botões padrões. Veja a posição desta classe na hierarquia wxPython:

wxObject
  wxEvtHandler
    wxWindow
      wxControl
        wxButton

Botões são geralmente colocados em caixas de diálogo e painéis. Vamos começar entendendo o construtor da classe wx.Button:

wx.Button(parent, id, label, pos, size=wxDefaultSize, 
  style=0, validator, name="button")

Este construtor segue a mesma ordem e estilo do construtor C++. Veja:

wxButton(wxWindow* parent, wxWindowID id, 
  const wxString& label = wxEmptyString, 
  const wxPoint& pos = wxDefaultPosition, const 
  wxSize& size = wxDefaultSize, long style = 0, 
  const wxValidator& validator = wxDefaultValidator,
  const wxString& name = "button")

Como podemos observar, vários parâmetros possuem valores padrões e, portanto, podem ser omitidos no momento da criação do componente. Veja um exemplo de como criar um wx.Button:

# Cria um botão e o adiciona no painel
btn = wx.Button(panel, label="Clique Aqui", 
  pos=(10, 10), size=(100, 25))

panel é uma referência a um wx.Panel, ou seja, o painel de conteúdo no qual o botão será anexado. Fornecer um componente pai do tipo painel (ou qualquer outro componente visível) é necessário para que o componente também seja visível na janela.

Link para compartilhar na Internet ou com seus amigos:

Python ::: Python para Engenharia ::: Geometria Analítica e Álgebra Linear

Como calcular o determinante de uma matriz 3x3 usando a Método de Sarrus em Python - Python para Álgebra Linear

Quantidade de visualizações: 5005 vezes

Os estudos da Geometria Analítica e Álgebra Linear envolvem, em boa parte de seus cálculos, a magnitude de vetores, ou seja, o módulo, tamanho, comprimento ou intensidade dos vetores. E isso não é diferente em relação às matrizes.

Quando uma matriz é envolvida nos cálculos, com muita frequência precisamos obter o seu determinante, que nada mais é que um número real associado à todas as matrizes quadradas.

Nesta dica mostrarei como obter o determinante de uma matriz quadrada de ordem 3, ou seja, três linhas e três colunas, usando o Método de Sarrus (somente matrizes 3x3). Note que é possível obter o mesmo resultado com o Teorema de Laplace, que não está restrito às matrizes quadradas de ordem 3. Veja também que não considerei as propriedades do determinante, o que, em alguns casos, simplifica muito os cálculos.

Então, vamos supor a seguinte matriz 3x3: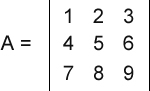

O primeiro passo é copiarmos a primeira e a segunda colunas para o lado direito da matriz. Assim: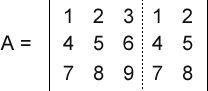

Agora dividimos a matriz em dois conjuntos: três linhas diagonais descendentes e três linhas diagonais ascendentes: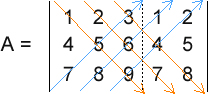

Agora é só efetuar cálculos. Multiplicamos e somamos os elementos de cada conjunto, subtraindo o segundo conjunto do primeiro. Veja:

(1 x 5 x 9 + 2 x 6 x 7 + 3 x 4 x 8) - (7 x 5 x 3 + 8 x 6 x 1 + 9 x 4 x 2) = 0

Como podemos ver, o determinante dessa matriz é 0.

E agora veja o código Python no qual declaramos e instanciamos uma matriz 3x3, em seguida, calculamos o seu determinante:

----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------

# importamos a bibliteca NumPy
import numpy as np

# função principal do programa
def main():
  # vamos criar uma matriz 3x3
  m = np.array([(1, 2, 3), (2, 5, 2), (1, 3, 1)])
  
  # calcula o determinante usando a Regra de Sarrus
  det = ((m[0][0] * m[1][1] * m[2][2]) + (m[0][1]  
    * m[1][2] * m[2][0]) + (m[0][2] * m[1][0] * m[2][1])) - ((m[2][0] 
    * m[1][1] * m[0][2]) + (m[2][1]  * m[1][2] * m[0][0]) + (m[2][2] 
    * m[1][0] * m[0][1]))
    
  # mostramos o resultado
  print("O determinante da matriz é: %f" % det)
  
if __name__== "__main__":
  main()

Ao executar este código Python nós teremos o seguinte resultado:

O determinante da matriz é: 2.0

É possível também obter o determinante de uma matriz (não restrita à dimensão 3x3) usando o método linalg.det() da biblioteca NumPy do Python. Veja o código a seguir:

----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------

# importamos a bibliteca NumPy
import numpy as np

# função principal do programa
def main():
  # vamos criar uma matriz 3x3
  m = np.array([(1, 2, 3), (2, 5, 2), (1, 3, 1)])
  
  # calcula o determinante usando apenas NumPy
  det = np.linalg.det(m)
    
  # mostramos o resultado
  print("O determinante da matriz é: %f" % det)
  
if __name__== "__main__":
  main()

Veja que usei a mesma matriz e, usando apenas o método linalg.det() nós obtemos o mesmo resultado.

Python ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas

Como calcular o seno de um número ou ângulo em Python usando a função sin() do módulo Math

Quantidade de visualizações: 1146 vezes

Em geral, quando falamos de seno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função seno disponível nas linguagens de programação para calcular o seno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria.

No entanto, é sempre importante entender o que é a função seno. Veja a seguinte imagem:

Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles.

Assim, o seno é a razão entre o cateto oposto (oposto ao ângulo theta) e a hipotenusa, ou seja, o cateto oposto dividido pela hipotenusa. Veja a fórmula:

\[\text{Seno} = \frac{\text{Cateto oposto}}{\text{Hipotenusa}} \]

Então, se dividirmos 20 por 36.056 (na figura eu arredondei) nós teremos 0.5547, que é a razão entre o cateto oposto e a hipotenusa (em radianos).

Agora, experimente calcular o arco-cosseno de 0.5547. O resultado será 0.9828 (em radianos). Convertendo 0.9828 radianos para graus, nós obtemos 56.31º, que é exatamente o ângulo em graus entre o cateto oposto e a hipotenusa na figura acima.

Pronto! Agora que já sabemos o que é seno na trigonometria, vamos entender mais sobre a função sin() da linguagem Python. Este método, que faz parte do módulo Math, recebe um valor numérico e retorna um valor, também numérico) entre -1 até 1 (ambos inclusos). Veja:

----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------

# importamos a biblioteca Math
import math as math
  
def main():
  print("Seno de 0 = ", math.sin(0))
  print("Seno de 1 = ", math.sin(1))
  print("Seno de 2 = ", math.sin(2))
  
if __name__== "__main__":
  main()

Ao executar este código Python nós teremos o seguinte resultado:

Seno de 0 = 0.0
Seno de 1 = 0.8414709848078965
Seno de 2 = 0.9092974268256817

Note que calculamos os senos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função seno mostrada abaixo:

Python ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas

Como calcular o comprimento da hipotenusa em Python dadas as medidas do cateto oposto e do cateto adjascente

Quantidade de visualizações: 1514 vezes

Nesta dica mostrarei como é possível usar a linguagem Python para retornar o comprimento da hipotenusa dadas as medidas do cateto oposto e do cateto adjascente. Vamos começar analisando a imagem a seguir:

Veja que, nessa imagem, eu já coloquei os comprimentos da hipotenusa, do cateto oposto e do cateto adjascente. Para facilitar a conferência dos cálculos, eu coloquei também os ângulos theta (que alguns livros chamam de alfa) e beta já devidamente calculados.

Então, sabendo que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos (Teorema de Pitógoras):

\[c^2 = a^2 + b^2\]

Tudo que temos a fazer a converter esta fórmula para código Python. Veja:

----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------

# vamos importar o módulo Math
import math as math

def main():
  a = 20 # medida do cateto oposto
  b = 30 # medida do cateto adjascente
  
  # agora vamos calcular o comprimento da hipotenusa
  c = math.sqrt(math.pow(a, 2) + math.pow(b, 2))
 
  # e mostramos o resultado
  print("O comprimento da hipotenusa é: %f" % c)
  
if __name__== "__main__":
  main()

Ao executar este código Python nós teremos o seguinte resultado:

O comprimento da hipotenusa é: 36.055513

Como podemos ver, o resultado retornado com o código Python confere com os valores da imagem apresentada.

Vamos testar seus conhecimentos em Fundações

Fundações profundas

As estacas Strauss podem ser armadas com ferragem longitudinal (barras retas) e estribos que permitam livre passagem do soquete de compactação e garantam um cobrimento da armadura não inferior a 3cm.

A estaca Strauss é recomendada:

A) apenas em terrenos com comprimento fixo de cravação.

B) em trabalhos abaixo do lençol freático.

C) em terrenos com comprimento variável de cravação.

D) com a disponibilidade de equipamentos robustos e complexos na execução.

E) em áreas não suscetíveis à presença de agentes biológicos.

Verificar Resposta Estudar Cards Todas as Questões

Vamos testar seus conhecimentos em JavaScript

Analise o seguinte código JavaScript

document.write(typeof NaN);

Qual é o resultado de sua execução?

A) undefined

B) null

C) number

D) NaN

E) string

Verificar Resposta Estudar Cards Todas as Questões

Vamos testar seus conhecimentos em Ética e Legislação Profissional

Responsabilidade civil dos prepostos e preponentes

De acordo com as definições de preposto gerente, assinale a alternativa correta.

A) O gerente é autorizado a praticar todos os atos necessários ao exercício dos poderes que lhe foram outorgados, mesmo que a lei exija poderes especiais para tal.

B) O gerente responde sozinho pelos atos praticados em seu nome e em nome do preponente.

C) O preponente pode estar em juízo em nome do gerente, pelas obrigações resultantes do exercício da sua função.

D) Considera-se gerente o preposto permanente no exercício da empresa, em sua sede, filial ou agência.

E) Os gerentes são responsáveis pelos atos dos preponentes, praticados nos seus estabelecimentos e relativos à atividade da empresa, ainda que não autorizados por escrito.

Verificar Resposta Estudar Cards Todas as Questões

Vamos testar seus conhecimentos em Python

Qual o resultado da execução do seguinte código Python?

frase = "Gosto Muito de Python"
frase = frase.swapcase()
print(frase)

A) gOSTO mUITO DE pYTHON

B) Gosto muito de python

C) Gosto Muito De Python

D) PYTHON DE MUITO GOSTO

E) gosto MUITO de PYTHON

Verificar Resposta Estudar Cards Todas as Questões

Vamos testar seus conhecimentos em

Dimensionamento de pilares de canto

Os pilares de canto são solicitados pela flexão oblíqua, tendo momentos de 1ª ordem e excentricidades nas direções x e y.

Analise os dados para o pilar a seguir:

Qual o valor das excentricidades no topo e na base do referido pilar, em x e y?

A) e1,x,A = 1,02cm.
e1,x,B = 1,31cm.
e1,y,A = 2,05cm.
e1,y,B = 1,75cm.

B) e1,x,A = 1,52cm.
e1,x,B = 1,31cm.
e1,y,A = 2,22cm.
e1,y,B = 1,99cm.

C) e1,x,A = 2,10cm.
e1,x,B = 1,56cm.
e1,y,A = 1,50cm.
e1,y,B = 1,99cm.

D) e1,x,A = 2,78cm.
e1,x,B = 1,32cm.
e1,y,A = 1,50cm.
e1,y,B = 1,99cm.

E) e1,x,A = 1,78cm.
e1,x,B = 1,32cm.
e1,y,A = 1,22cm.
e1,y,B = 0,99cm.

Verificar Resposta Estudar Cards Todas as Questões

Desafios, Exercícios e Algoritmos Resolvidos de Python

Escreva um programa Python que lê inteiros informados pelo usuário e os armazena em uma lista. Seu programa deverá - Exercícios Resolvidos de Python

Escreva um programa Python que pede um número inteiro e informa se o número informado é um número de Armstrong - Exercício Resolvido de Python

Como criar uma List de Alunos, inserir novos alunos e listá-los usando um menu de opções - Exercícios Resolvidos de Python

Escreva um programa Python que leia os elementos de um vetor A de dez elementos inteiros e construa outro vetor B - Exercício Resolvido de Python

Exercício Resolvido de Python Pandas - Como retornar a coluna com o maior número de valores ausentes em um DataFrame - Exercícios Resolvidos de Python

Como testar se um número é positivo ou negativo em Python - Exercícios Resolvidos de Python

Como calcular a média aritmética, ponderada e harmônica em Python - Escreva um programa Python que receba as 3 notas - Exercícios Resolvidos de Python

Como somar todos os números de 1 até o número informado pelo usuário em Python - Exercício Resolvido de Python

Desafio do número ausente. Dado um vetor de números naturais 1..n, encontre o valor ausente - Exercício Resolvido de Python

Como testar se duas palavras são anagramas uma da outra - Solução usando dicionário/hash table - Exercícios Resolvidos de Python

Ler um número de três dígitos, separá-lo e invertê-lo, escrevendo o número lido e sua forma inversa - Exercício Resolvido de Python

Como retornar o maior elemento em cada uma das colunas de uma matriz usando Python - Exercícios Resolvidos de Python

Como calcular a área de um losango em Python - Exercícios Resolvidos de Python

Peça para o usuário informar o valor do primeiro elemento e gere os valores dos demais elementos com o dobro do - Exercício Resolvido de Python

Como calcular o peso de uma pessoa na Lua usando Python - Exercícios Resolvidos de Python

Como calcular as reações de apoio, momento de flexão máxima e forças cortantes em uma viga bi-apoiada com carga distribuída retangular usando Python - Exercício Resolvido de Python

O Sr. João necessita saber o consumo médio de um automóvel, e solicitou para você desenvolver um algoritmo Python que - Exercício Resolvido de Python

Exercícios Resolvidos de Física usando Python - Calcule a resistência elétrica de um resistor que apresenta 10 A - Exercício Resolvido de Python

Uma classe para representar uma pessoa, com os atributos privados de nome, data de nascimento e altura - Exercício Resolvido de Python

Escrever um algoritmo que leia o nome de um aluno e as notas das três provas que ele obteve no semestre. No final informar o nome do aluno - Exercícios Resolvidos de Python

Como converter minutos em segundos usando Python - Exercícios Resolvidos de Python

Escreva um programa Python para exibir a soma dos cubos de dois números informados pelo usuário. Faça a leitura da entrada do usuário - Exercício Resolvido de Python

Como transformar dias em anos, meses, semanas e dias em Python - Exercício Resolvido de Python

Como exibir a data e hora atual usando Python - Exercício Resolvido de Python

Uma locadora de carros aluga seus veículos cobrando uma taxa de R$ 25,00 reais a diária mais R$ 0,20 por quilômetro rodado - Exercícios Resolvidos de Python

Um programa Python que calcula qual o menor número possível de notas de 100, 50, 10, 5 e 1 em que o valor a ser sacado pode ser decomposto - Exercícios Resolvidos de Python

Exercícios Resolvidos de Física usando Python - Aplica-se uma força de 20 N a um corpo de massa m. O corpo desloca-se em linha reta com velocidade que aumenta - Exercício Resolvido de Python

Crie uma classe Circulo que possui um construtor que receberá o valor do raio. Inclua um método getArea() para calcular - Exercício Resolvido de Python

Escreva um programa Python para encontrar o segundo maior valor em um vetor de inteiros - Exercício Resolvido de Python

As maçãs custam R$ 0,30 cada se forem compradas menos do que uma dúzia, e R$ 0,25 se forem compradas pelo menos doze - Exercício Resolvido de Python

Veja mais Dicas e truques de Python

Exercício Resolvido de Python NumPy - Como converter uma matriz de binários em uma matriz de booleanos usando Python e NumPy

Exercícios Resolvidos de Python - Uma locadora de charretes cobra R$ 10,00 de taxa para cada 3 horas de uso destas

Como gerar vetores e matrizes com números inteiros aleatórios usando a função random.randint() da biblioteca NumPy para - Machine Learning com Python

Como retornar o resultado de uma divisão de inteiros, incluindo o resto, em Python, usando a função divmod() do Python

Exercícios Resolvidos de Python - A empresa GÁS TOTAL paga uma gratificação de R$ 237,50 a todos os seus funcionários. Escreva um programa Python

Como pesquisar uma palavra em um arquivo texto usando Python

Exercícios Resolvidos de Python - Como verificar quantas vezes um valor é encontrado em um vetor - Como usar vetores e matrizes em Python

Exercício Resolvido de Python - Como calcular a média aritmética, ponderada e harmônica em Python - Escreva um programa Python que receba as 3 notas

Como testar se um diretório está vazio usando Python

Como converter metros em pés em Python - Conversão de medidas em Python - Metros para pés

Dicas e truques de outras linguagens

HTML5 - Programação gráfica para iniciantes - Como desenhar círculos com ou sem preenchimento usando o método arc() do objeto Canvas do HTML5

Java - Como passar vetores e matrizes (arrays) para seus métodos Java

Python - Exercícios Resolvidos de Python - Como escrever uma função Python que recebe dois números inteiros e retorna a soma desses dois valores como um inteiro

Ruby - Como trabalhar com strings em Ruby

Java - Como inverter uma string em Java usando o método reverse() da classe StringBuffer

Python - Como embaralhar os elementos de um array em Python usando random.shuffle()

Java - Exercícios Resolvidos de Java - Um programa Java que gera um número randômico na faixa de 20 a 40 (valores inclusos) e exibe o seno, cosseno e tangente

Python - Como verificar se uma string contém apenas caracteres de espaços em Python usando a função isspace()

JavaScript - Como adicionar um ou mais elementos ao início de um vetor JavaScript usando o método unshift() do objeto Array - [Revisado]

Java - Como calcular o seno de um número ou ângulo em Java usando o método sin() da classe Math

Códigos Fonte

Programa de Gestão Financeira Controle de Contas a Pagar e a Receber com Cadastro de Clientes e Fornecedores

Software de Gestão Financeira com código fonte em PHP, MySQL, Bootstrap, jQuery - Inclui cadastro de clientes, fornecedores e ticket de atendimento
Diga adeus às planilhas do Excel e tenha 100% de controle sobre suas contas a pagar e a receber, gestão de receitas e despesas, cadastro de clientes e fornecedores com fotos e histórico de atendimentos. Código fonte completo e funcional, com instruções para instalação e configuração do banco de dados MySQL. Fácil de modificar e adicionar novas funcionalidades. Clique aqui e saiba mais

Controle de Estoque completo com código fonte em PHP, MySQL, Bootstrap, jQuery - 100% funcional e fácil de modificar e implementar novas funcionalidades
Tenha o seu próprio sistema de controle de estoque web. com cadastro de produtos, categorias, fornecedores, entradas e saídas de produtos, com relatórios por data, margem de lucro e muito mais. Código simples e fácil de modificar. Acompanha instruções para instalação e criação do banco de dados MySQL. Clique aqui e saiba mais

Linguagens Mais Populares

1º lugar: Java
2º lugar: Python
3º lugar: C#
4º lugar: PHP
5º lugar: Delphi
6º lugar: C
7º lugar: JavaScript
8º lugar: C++
9º lugar: VB.NET
10º lugar: Ruby

Você está aqui: Python ::: wxPython ::: wxButton

Entenda e aprenda a usar a classe wx.Button

Python ::: Python para Engenharia ::: Geometria Analítica e Álgebra Linear

Como calcular o determinante de uma matriz 3x3 usando a Método de Sarrus em Python - Python para Álgebra Linear

Python ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas

Como calcular o seno de um número ou ângulo em Python usando a função sin() do módulo Math

Python ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas

Como calcular o comprimento da hipotenusa em Python dadas as medidas do cateto oposto e do cateto adjascente

Vamos testar seus conhecimentos em Fundações

Vamos testar seus conhecimentos em JavaScript

Vamos testar seus conhecimentos em Ética e Legislação Profissional

Vamos testar seus conhecimentos em Python

Vamos testar seus conhecimentos em

Questões de Concurso para Engenharia Civil

Exercícios Resolvidos

Bancos de Dados

Questões de Concurso

Frameworks

Projetos e Códigos Fonte

Especializações

Calculadoras

Ferramentas

Todas as Linguagens, Frameworks, Biliotecas e Bancos de Dados

Compre pelo WhatsApp: +55 (062) 98553-6711

E-Book 650 Dicas e Truques de Python - Com comentários em Português

PDF COM 1.200 PÁGINAS

Apenas R$ 32,90