Você está aqui: Python ::: Dicas & Truques ::: Data e Hora |
Obtendo o número da semana no ano (domingo como primeiro dia da semana)Quantidade de visualizações: 10831 vezes |
# -*- coding: UTF-8 -*-
"""
Este exemplo mostra como exibir o número
da semana no ano, tomando o domingo como
primeiro dia da semana. Todos os dias
antes do primeiro domingo do ano são considerados
como semana 0. O intervalo do valor retornado
é 00-53.
"""
from datetime import datetime
# Obtém um datetime da data e hora atual
hoje = datetime.today()
# Exibe o número da semana como um decimal
print hoje.strftime("O número da semana é: %U")
|
|
|
Python ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cosseno de um ângulo em Python usando a função cos() do módulo Math - Calculadora de cosseno em PythonQuantidade de visualizações: 2525 vezes |
|
Como calcular o cosseno de um ângulo em Python usando a função cos() do módulo Math - Calculadora de cosseno em Python Em geral, quando falamos de cosseno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função cosseno disponível nas linguagens de programação para calcular o cosseno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função cosseno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o cosseno é a razão entre o cateto adjascente e a hipotenusa, ou seja, o cateto adjascente dividido pela hipotenusa. Veja a fórmula: \[\text{Cosseno} = \frac{\text{Cateto adjascente}}{\text{Hipotenusa}} \] Então, se dividirmos 30 por 36.056 (na figura eu arredondei) nós teremos 0.8320, que é a razão entre o cateto adjascente e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.8320. O resultado será 0.5881 (em radianos). Convertendo 0.5881 radianos para graus, nós obtemos 33.69º, que é exatamente o ângulo em graus entre o cateto adjascente e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é cosseno na trigonometria, vamos entender mais sobre a função cos() da linguagem Python. Esta função, que faz parte do módulo Math, recebe um valor numérico float e retorna um valor float, ou seja, também numérico) entre -1 até 1 (ambos inclusos). Veja: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# vamos importar o módulo Math
import math as math
def main():
# vamos calcular o cosseno de três números
print("Cosseno de 0 = %f" % math.cos(0))
print("Cosseno de 1 = %f" % math.cos(1))
print("Cosseno de 2 = %f" % math.cos(2))
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Cosseno de 0 = 1.000000 Cosseno de 1 = 0.540302 Cosseno de 2 = -0.416147 Note que calculamos os cossenos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função cosseno mostrada abaixo: 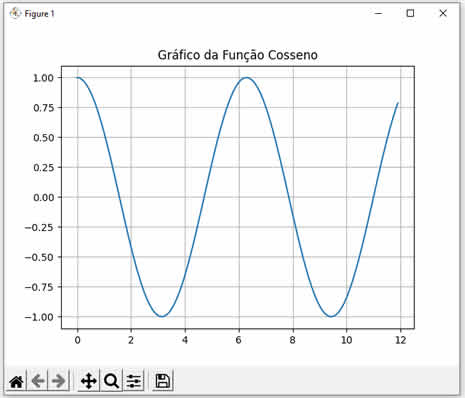 |
Python ::: Dicas & Truques ::: Strings e Caracteres |
Como verificar se uma string é composta apenas de caracteres maiúsculos usando a função isupper() do PythonQuantidade de visualizações: 9068 vezes |
|
Este exemplo mostra como usar a função isupper() do objeto string da linguagem Python para verificar se uma palavra, frase ou texto contém apenas caracteres maiúsculos. Se qualquer caractere minúsculo for encontrado, a função retorna false. Obs: Mesmo que a string contenha números ela ainda pode estar em letras maiúsculas. Veja um código Python completo exemplificando seu uso: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
def main():
string = "GOSTO DE PYTHON E JAVA"
if string.isupper():
print("A string está em letras maiúsculas")
else:
print("A string não está em letras maiúsculas")
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: A string está em letras maiúsculas |
Python ::: Desafios e Lista de Exercícios Resolvidos ::: Ordenação e Pesquisa (Busca) |
Exercícios Resolvidos de Python - Como usar a Ordenação da Bolha em Python para ordenar os valores de um vetor em ordem crescente ou decrescenteQuantidade de visualizações: 566 vezes |
|
Pergunta/Tarefa: A Ordenação da Bolha, ou ordenação por flutuação (literalmente "por bolha"), também chamada de Bubble Sort, é um algoritmo de ordenação dos mais simples. A ideia é percorrer o array diversas vezes, a cada passagem fazendo flutuar para o topo o maior elemento da sequência. Essa movimentação lembra a forma como as bolhas em um tanque de água procuram seu próprio nível, e disso vem o nome do algoritmo. No melhor caso, o algoritmo executa n operações relevantes, onde n representa o número de elementos do vetor. No pior caso, são feitas n2 operações. A complexidade desse algoritmo é de ordem quadrática. Por isso, ele não é recomendado para programas que precisem de velocidade e operem com quantidade elevada de dados. Escreva um programa Python que declara, constrói um vetor de 10 inteiros e peça para o usuário informar os valores de seus elementos. Em seguida use a ordenação da bolha para ordenar os elementos em ordem crescente. Sua saída deverá ser parecida com: Informe o valor para o índice 0: 84 Informe o valor para o índice 1: 23 Informe o valor para o índice 2: 9 Informe o valor para o índice 3: 5 Informe o valor para o índice 4: 11 Informe o valor para o índice 5: 3 Informe o valor para o índice 6: 50 Informe o valor para o índice 7: 7 Informe o valor para o índice 8: 2 Informe o valor para o índice 9: 73 O array informado foi: 84 23 9 5 11 3 50 7 2 73 O array ordenado é: 2 3 5 7 9 11 23 50 73 84 Veja a resolução comentada deste exercício usando Python: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# função principal do programa
def main():
# vamos declarar e construir um vetor de 10 elementos
valores = [0 for x in range(10)]
# vamos pedir que o usuário informe os valores
for i in range(0, len(valores)):
valores[i] = int(input("Informe o valor para o índice {0}: ".format(i)))
# vamos mostrar o vetor informado
print("\nO array informado foi:\n\n")
for i in range(0, len(valores)):
print(valores[i], end=" ")
# vamos ordenar os elementos do vetor usando a ordenação da bolha
# laço externo de trás para frente
for i in range(len(valores) - 1, 0, -1):
for j in range(0, i): # laço interno vai no fluxo normal
if valores[j] > valores[j + 1]: # temos que trocá-los de lugar
temp = valores[j]
valores[j] = valores[j + 1]
valores[j + 1] = temp
# vamos exibir o vetor já ordenado
print("\n\nO array ordenado é:\n\n")
for i in range(0, len(valores)):
print(valores[i], end=" ")
print("\n")
if __name__== "__main__":
main()
|
Python ::: Flask Micro Framework ::: Rotas e Roteamento |
Como criar rotas em suas aplicações Flask usando o decorador @app.route() - Tutorial Flask para iniciantesQuantidade de visualizações: 1553 vezes |
|
Aplicações web modernas usam uma técnica chamada roteamento nomeado, ou, na linguagem do pessoal do SEO, URLs amigáveis. Isso quer dizer que, em vez de termos URLS do tipo /livro.php?id_livro=39 nós temos /livro/39. Neste modelo de roteamento, livro é o nome de uma função Python que será chamada quando o usuário acessar este endereço, e 39 será o argumento passado para o método. Em Flask, as URLs são associadas às funções Python por meio do decorador @app.route(). Veja uma aplicação Flask completa que possui um método index() que é chamado quando o usuário acessa a raiz da aplicação: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# vamos importar a biblioteca Flask
from flask import Flask
# função principal do programa
def main():
# vamos criar a aplicação Flask
app = Flask(__name__)
# definimos a rota para a função index()
@app.route("/")
def index():
return "Este é o método index()"
# e iniciamos a aplicação web na porta 5000
app.run(port=5000, debug=True)
if __name__== "__main__":
main()
Note que a nossa aplicação Flask estará disponível na porta 5000. Assim, ao acessar o endereço http://127.0.0.1:5000 nós teremos o seguinte resultado: Este é o método index() Veja agora como criar uma URL /listar_usuarios e associá-la a uma função listar_usuarios(): ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# vamos importar a biblioteca Flask
from flask import Flask
# função principal do programa
def main():
# vamos criar a aplicação Flask
app = Flask(__name__)
# definimos a rota para a função index()
@app.route("/")
def index():
return "Este é o método index()"
# definimos a rota para a função listar_usuarios()
@app.route("/listar_usuarios")
def listar_usuarios():
return "Este é o método para listar os usuários"
# e iniciamos a aplicação web na porta 5000
app.run(port=5000, debug=True)
if __name__== "__main__":
main()
Agora, experimente acessar o endereço http://127.0.0.1:5000/listar_usuarios e veja o resultado. Se tudo estiver correto, você verá o seguinte resultado: Este é o método para listar os usuários Em mais dicas desta seção você verá como criar URLs com parâmetros e passá-los para suas funções Python. |
Python ::: Dicas & Truques ::: Strings e Caracteres |
Como pesquisar substrings em strings usando a função index() da linguagem PythonQuantidade de visualizações: 8468 vezes |
Este exemplo mostra como pesquisar uma substring em uma string usando o método index() do Python. A assinatura desta função é:index(substring[, start[, end]]) onde substring é a substring a ser pesquisada e start e end são argumentos opcionais que definem os índices de início e fim da pesquisa. Se a substring não for encontrada, uma exceção do tipo ValueError é levantada. Se for encontrada, o índice do primeiro caractere é retornado. Veja o código Python completo para a dica: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
def main():
frase = "Gosto de Python e JavaScript"
try:
indice = frase.index("Python")
except ValueError:
print("A palavra não foi encontrada")
else:
print("A palavra foi encontrada no índice", indice)
if __name__== "__main__":
main()
Ao executarmos este código Python nós teremos o seguinte resultado: A palavra foi encontrada no índice 9. |
Python ::: Dicas & Truques ::: Matemática e Estatística |
Como calcular desvio padrão em Python - Python para Matemática e EstatísticaQuantidade de visualizações: 5075 vezes |
|
Em Matemática e Estatística, o Desvio padrão (em inglês: Standard Deviation) é uma medida de dispersão, ou seja, é uma medida que indica o quanto um conjunto de dados é uniforme. Quando o desvio padrão é baixo, isso quer dizer que os dados do conjunto estão mais próximos da média. Como calcular o desvio padrão de um conjunto de dados? Vamos começar analisando a fórmula mais difundida na matemática e na estatística: \[\sigma = \sqrt{ \frac{\sum_{i=1}^N (x_i -\mu)^2}{N}}\] Onde: a) __$\sigma__$ é o desvio; b) __$x_i__$ é um valor qualquer no conjunto de dados na posição i; c) __$\mu__$ é a média aritmética dos valores do conjunto de dados; d) N é a quantidade de valores no conjunto. O somatório dentro da raiz quadrada nos diz que devemos somar todos os elementos do conjunto, desde a posição 1 até a posição n, subtrair cada valor pela média do conjunto e elevar ao quadrado. Obtida a soma, nós a dividimos pelo tamanho do conjunto. Veja o código Python completo que obtém o desvio padrão a partir de um conjunto de dados contendo quatro valores: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# precisamos importar o módulo Math
import math
# função principal do programa
def main():
# conjunto dos dados
conjunto = [10, 30, 90, 30]
soma = 0.0 # soma dos elementos
desvio_padrao = 0.0 # desvio padrão
tam = len(conjunto) # tamanho dos dados
# vamos somar todos os elementos
for i in range(0, tam):
soma = soma + conjunto[i]
# agora obtemos a média do conjunto de dados
media = soma / tam
# e finalmente obtemos o desvio padrão
for i in range(0, tam):
desvio_padrao = desvio_padrao + math.pow(conjunto[i] - media, 2)
# mostramos o resultado
print("Desvio Padrão Populacional: {0}".format(math.sqrt(desvio_padrao / tam)))
print("Desvio Padrão Amostral: {0}".format(math.sqrt(desvio_padrao / (tam - 1))))
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Desvio Padrão Populacional: 30.0 Desvio Padrão Amostral: 34.64101615137755 Veja que, para calcular o Desvio Padrão Populacional, nós dividimos o somatório pela quantidade de elementos no conjunto, enquanto, para calcular o Desvio Padrão Amostral, nós dividimos o somatório pela quantidade de elementos - 1 (cuidado com a divisão por zero no caso de um conjunto com apenas um elemento). |
Python ::: Desafios e Lista de Exercícios Resolvidos ::: Hidrologia e Hidráulica |
Exercícios Resolvidos de Python - FEMPERJ-2012-TCE-RJ: A vazão de dimensionamento de uma galeria de águas pluviais que drena uma área densamente urbanizada de 10 hectaresQuantidade de visualizações: 368 vezes |
|
Pergunta/Tarefa: 1) FEMPERJ-2012-TCE-RJ: A vazão de dimensionamento de uma galeria de águas pluviais que drena uma área densamente urbanizada de 10 hectares, considerando-se uma chuva de projeto com intensidade de 60 mm/hora, duração igual ao tempo de concentração da bacia e coeficiente de escoamento superficial igual a 0,90, através do Método Racional, é: A) 150 m3/s B) 0,150 l/s C) 1,5 m3/s D) 150 l/s E) 15 m3/s Sua saída deve ser parecida com: Intensidade da chuva em mm/h: 60 Área da bacia em hectares: 10 Coeficiente de escoamento: 0.9 A vazão de dimensionamento é: 1.5 m3/s O primeiro passo para resolver esta questão é relembrar a fórmula da Vazão pelo Método Racional. Apresentado pela primeira vez em 1851 por Mulvaney e usado por Emil Kuichling em 1889, o Método Racional é um método indireto e estabelece uma relação entre a chuva e o escoamento superficial (deflúvio). Usamos esta fórmula para calcular a vazão de pico de uma determinada bacia, considerando uma seção de estudo. Eis a fórmula: \[Q = \frac{C \cdot I \cdot A}{360} \] Onde: Q = vazão de pico (m3/s); C = coeficiente de escoamento superficial que varia de 0 a 1. Coeficiente de Runoff (adimensional). I = intensidade média da chuva (mm/h); A = área da bacia (ha), onde 1 ha = 10.000m2. A [[menor_igual]] 300 ha. Na questão do concurso nós já temos a intensidade da chuva em milímetros por hora e a área já está em hectares. Tudo que temos a fazer é jogar na fórmula. Então, hora de vermos a resolução comentada deste exercício usando Python: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# função principal do programa
def main():
# vamos ler a precipitação ou intensidade da chuva em mm/h
intensidade = float(input("Intensidade da chuva em mm/h: "))
# vamos ler a área da bacia em hectares
area_bacia = float(input("Área da bacia em hectares: "))
# vamos ler o coeficiente de escoamento
coeficiente = float(input("Coeficiente de escoamento: "))
# e vamos calcular a vazão de pico em metros cúbicos
vazao = ((coeficiente * intensidade * area_bacia) / 360.0)
# e mostramos o resultado
print("A vazão de dimensionamento é: {0} m3/s".format(vazao))
if __name__== "__main__":
main()
|
Python ::: Desafios e Lista de Exercícios Resolvidos ::: Python Básico |
Exercícios Resolvidos de Python - Escreva um programa em Python que usa a função log10() para informar a quantidade de dígitos em um número inteiroQuantidade de visualizações: 587 vezes |
|
Pergunta/Tarefa: Escreva um algorítmo em Python que peça para o usuário informar um número inteiro de qualquer tamanho, ou seja, qualquer quantidade de dígitos. Em seguida seu código deverá informar a quantidade de dígitos contida no número inteiro digitado pelo usuário. Seu programa deverá, obrigatoriamente, usar a função log10() do módulo Math. Sua saída deverá ser parecida com: Informe um número inteiro de qualquer tamanho: 847 O número informado possui 3 dígitos Veja a resolução comentada deste exercício usando Python: ----------------------------------------------------------------------
Se precisar de ajuda para ajustar o código abaixo de acordo com as
suas necessidades, chama a gente no WhatsApp +55 (62) 98553-6711 (Osmar)
Ah, e se puder, faça uma DOAÇÃO de qualquer valor para nos ajudar
a manter o site livre de anúncios. Ficaremos eternamente gratos ;-)
Nosso PIX é: osmar@arquivodecodigos.com.br
----------------------------------------------------------------------
# vamos importar o módulo Math
import math
# método principal
def main():
# vamos pedir para o usuário informar um número inteiro
numero = int(input("Informe um número inteiro de qualquer tamanho: "))
# agora vamos obter a quantidade de dígitos no
# número informado
tamanho = int(math.log10(numero)) + 1
# mostramos o resultado
print("O número informado possui {0} dígitos".format(tamanho))
if __name__== "__main__":
main()
|
Vamos testar seus conhecimentos em |
| Características do concreto armado A reologia é o ramo da mecânica que estuda a evolução de deformações de um material por causas tencionais ao longo do tempo. O fenômeno reológico que independe do carregamento e ocorre devido à variação de umidade do concreto, gerando deformações diferenciais e tensões internas aos elementos de concreto, pode ser classificado como: A) fissuração. B) retração. C) fluência. D) deformação lenta. E) variação de temperatura. Verificar Resposta Estudar Cards Todas as Questões |
Vamos testar seus conhecimentos em Hidrostática |
| Princípios da Hidrostática Calcule a pressão causada por uma determinada caixa de madeira cujo peso vale 12N e cujas dimensões retangulares da base medem 15cm de comprimento e 5cm de largura. A) 1000Pa. B) 1600Pa. C) 2300Pa. D) 3200Pa. E) 4500Pa. Verificar Resposta Estudar Cards Todas as Questões |
Vamos testar seus conhecimentos em Python |
Analise o seguinte código Python
a = {5, 8, 2, 1}
b = {1, 4, 5, 3}
c = a & b
print(c)
Qual é o resultado de sua execução? A) {5, 5, 1, 1} B) Um erro de execução na linha 2 C) {1, 5} D) {5, 8, 2, 1, 1, 4, 5, 3} Verificar Resposta Estudar Cards Todas as Questões |
Vamos testar seus conhecimentos em JavaScript |
| JavaScript é o mesmo que Java? A) Sim B) Não Verificar Resposta Estudar Cards Todas as Questões |
Vamos testar seus conhecimentos em |
| Vidros Qual dos tipos abaixo não é um vidro: A) Soda-cálcico. B) Boro-silicato. C) Ao chumbo. D) Quartzitos. E) Alumínio borosilicato. Verificar Resposta Estudar Cards Todas as Questões |
Mais Desafios de Programação e Exercícios e Algoritmos Resolvidos de Python |
Veja mais Dicas e truques de Python |
Dicas e truques de outras linguagens |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |






