Você está aqui: Cards de Python |
||
|
||
|
|
||
C++ ::: Dicas & Truques ::: Arquivos e Diretórios |
Como renomear um diretório em C++ usando a função rename()Quantidade de visualizações: 8742 vezes |
Em algumas situações nossos códigos C++ precisam renomear diretórios. Isso pode ser feito com o auxílio da função rename() ou _rename(), disponível no header io.h or stdio.h (trazido da linguagem C). Veja a assinatura desta função:int rename(const char *oldname, const char *newname); Se o diretório for renomeado com sucesso a função retornará o valor 0. O retorno será -1 se um erro ocorrer. Neste caso a variável global errno será definido como um dos seguintes valores: a) EINVAL - Invalid argument - Os nomes dos diretórios contém caracteres inválidos; b) ENOENT - No such file or directory - O caminho do diretório é inválido; c) EACCESS - Acesso negado - Algum outro programa está usando este diretório e mantém controle sobre o mesmo. Veja um trecho de código no qual renomeamos um diretório:
#include <iostream>
using namespace std;
int main(int argc, char *argv[]){
// vamos renomear este diretório
char dir_antigo[] = "C:\\Dev-Cpp\\estudos";
char dir_novo[] = "C:\\Dev-Cpp\\estudos2";
// vamos testar se o diretório for renomeado com sucesso
if(rename(dir_antigo, dir_novo) != 0){
cout << "Erro: " << strerror(errno) << endl;
}
else{
cout << "Diretório renomeado com sucesso" << endl;
}
system("PAUSE"); // pausa o programa
return EXIT_SUCCESS;
}
É possível usar a versão Unicode de rename() ou _rename(). O método _wrename, também presente em io.h or stdio.h é útil quando precisamos internacionalizar nossas aplicações. Veja o exemplo:
#include <iostream>
using namespace std;
int main(int argc, char *argv[]){
// vamos renomear este diretório
wchar_t dir_antigo[] = L"C:\\Dev-Cpp\\estudos";
wchar_t dir_novo[] = L"C:\\Dev-Cpp\\estudos2";
// vamos testar se o diretório for renomeado com sucesso
if(_wrename(dir_antigo, dir_novo) != 0){
cout << "Erro: " << strerror(errno) << endl;
}
else{
cout << "Diretório renomeado com sucesso" << endl;
}
system("PAUSE"); // pausa o programa
return EXIT_SUCCESS;
}
Ao executar este código C++ nós teremos o seguinte resultado: Diretório renomeado com sucesso |
C# ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cosseno de um ângulo em C# usando a função Cos() da classe Math - Calculadora de cosseno em C#Quantidade de visualizações: 2490 vezes |
|
Em geral, quando falamos de cosseno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função cosseno disponível nas linguagens de programação para calcular o cosseno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função cosseno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o cosseno é a razão entre o cateto adjascente e a hipotenusa, ou seja, o cateto adjascente dividido pela hipotenusa. Veja a fórmula: \[\text{Cosseno} = \frac{\text{Cateto adjascente}}{\text{Hipotenusa}} \] Então, se dividirmos 30 por 36.056 (na figura eu arredondei) nós teremos 0.8320, que é a razão entre o cateto adjascente e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.8320. O resultado será 0.5881 (em radianos). Convertendo 0.5881 radianos para graus, nós obtemos 33.69º, que é exatamente o ângulo em graus entre o cateto adjascente e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é cosseno na trigonometria, vamos entender mais sobre a função Cos() da linguagem C#. Esta função, que é um método da classe Math, recebe um valor numérico Double e retorna um valor Double, ou seja, também numérico) entre -1 até 1 (ambos inclusos). Veja:
using System;
using System.Collections;
namespace Estudos {
class Program {
static void Main(string[] args) {
// vamos calcular o cosseno de três números
Console.WriteLine("Cosseno de 0 = " + Math.Cos(0));
Console.WriteLine("Cosseno de 1 = " + Math.Cos(1));
Console.WriteLine("Cosseno de 2 = " + Math.Cos(2));
Console.WriteLine("\nPressione qualquer tecla para sair...");
// pausa o programa
Console.ReadKey();
}
}
}
Ao executar este código C# nós teremos o seguinte resultado: Cosseno de 0 = 1 Cosseno de 1 = 0,5403023058681397 Cosseno de 2 = -0,4161468365471424 Note que calculamos os cossenos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função cosseno mostrada abaixo: 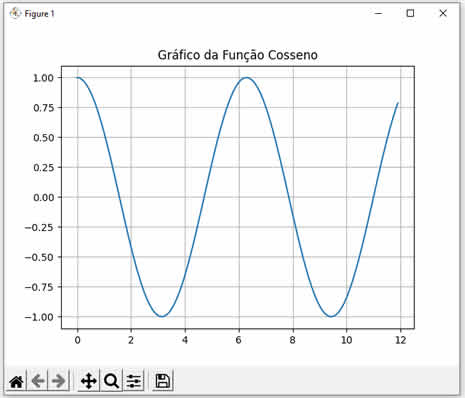 |
LISP ::: Desafios e Lista de Exercícios Resolvidos ::: Estruturas de Controle |
Exercícios Resolvidos de LISP - Um programa que lê duas notas, calcula a média aritmética e exibe uma mensagem de reprovado, exame ou aprovadoQuantidade de visualizações: 649 vezes |
|
Pergunta/Tarefa: Escreva um programa LISP ou Common Lisp que leia duas notas (como double ou float), calcule e mostre a média aritmética e uma mensagem de acordo com as seguintes regras: 1) Se a média for inferior a 4,0 escreva "Reprovado"; 2) Se a média for igual ou superior a 4,0 e inferior a 7,0 escreva "Exame"; 3) Se a média for igual ou superior a 7,0 escreva "Aprovado". Sua saída deverá ser parecida com: Informe a primeira nota: 8 Informe a segunda nota: 7.4 A média obtida foi: 7.7 Aprovado Veja a resolução comentada deste exercício usando Common Lisp (a padronização da linguagem LISP):
; Algoritmo LISP para calcular a média de um aluno
; variáveis que vamos usar no programa
(let ((n1)(n2)(media))
; vamos solicitar as duas notas do aluno
(princ "Informe a primeira nota: ")
(force-output)
(setq n1 (read))
(princ "Informe a segunda nota: ")
(force-output)
(setq n2 (read))
; vamos calcular a média aritmética
(setq media (/ (+ n1 n2) 2))
(format t "A média obtida foi ~F" media)
; vamos verificar se o aluno foi reprovado, está de exame ou aprovado
(cond
((< media 4.0) ; reprovado
(format t "~%Reprovado"))
((and (>= media 4.0)(< media 7.0)) ; exame
(format t "~%Exame"))
(t (format t "~%Aprovado"))
)
)
|
Portugol ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em Portugol dados dois pontos no plano cartesianoQuantidade de visualizações: 770 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem Portugol que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
// Calcular o coeficiente angular de uma reta em Portugol
programa {
// vamos incluir a biblioteca Matematica
inclua biblioteca Matematica --> mat
funcao inicio() {
// coordenadas dos dois pontos
real x1, y1, x2, y2
// guarda o coeficiente angular
real m
// x e y do primeiro ponto
escreva("Coordenada x do primeiro ponto: ")
leia(x1)
escreva("Coordenada y do primeiro ponto: ")
leia(y1)
// x e y do segundo ponto
escreva("Coordenada x do segundo ponto: ")
leia(x2)
escreva("Coordenada y do segundo ponto: ")
leia(y2)
// vamos calcular o coeficiente angular
m = (y2 - y1) / (x2 - x1)
// mostramos o resultado
escreva("O coeficiente angular é: ", m)
}
}
Ao executar este código Portugol Webstudio nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 3 Coordenada y do primeiro ponto: 6 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 10 O coeficiente angular é: 0.6666666666666666 No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Estruturas de Controle |
Exercícios Resolvidos de Java - Como criar um conversor de moedas em Java - Um programa Java para converter de Real para Dólar e de Dólar para RealQuantidade de visualizações: 2655 vezes |
|
Pergunta/Tarefa: Escreva um programa Java para converter de Real para Dólar e vice-versa. Seu programa deverá ler o valor a ser convertido e a opção de conversão, ou seja, se o usuário quer converter de Real para Dólar ou se quer converter de Dólar para Real. Em seguida mostre o valor convertido. Você pode pedir também a cotação do Dólar ou já deixar definido no código. Na resolução eu fixei a cotação no código mesmo, tomando como base a cotação do Dólar na data 20/02/2023. Sua saída deverá ser parecida com: Valor a ser convertido: 7 1. Converter de Real para Dólar 2. Converter de Dólar para Real Sua opção: 1 O valor convertido para Dólar é: $ 1,28 Valor a ser convertido: 1 1. Converter de Real para Dólar 2. Converter de Dólar para Real Sua opção: 2 O valor convertido para Real é: R$ 5,46 Veja a resolução comentada deste exercício usando Java:
package estudos;
import java.util.Scanner;
public class Estudos {
public static void main(String[] args) {
// vamos registrar aqui a cotaçao do dólar
double cotacao_dolar = 5.4613; // 20/02/2023
// valor informado e valor convertido
double valor, valor_convertido;
// para ler a opção do usuário
int opcao;
// para ler a entrada do usuário
Scanner entrada = new Scanner(System.in);
// vamos pedir para o usuário informar o valor a ser convertido
System.out.print("Valor a ser convertido: ");
valor = Double.parseDouble(entrada.nextLine());
// vamos mostrar as opções de conversão
System.out.println("\n1. Converter de Real para Dólar");
System.out.println("2. Converter de Dólar para Real");
System.out.print("Sua opção: ");
opcao = Integer.parseInt(entrada.nextLine());
// vamos fazer a conversão entre as moedas
switch(opcao){
case 1: // efetua a conversão de Real para Dólar
valor_convertido = valor / cotacao_dolar;
System.out.printf("\nO valor convertido para Dólar é: $ %.2f\n\n",
valor_convertido);
break;
case 2: // efetua a conversão de Dólar para Real
valor_convertido = valor * cotacao_dolar;
System.out.printf("\nO valor convertido para Real é: R$ %.2f\n\n",
valor_convertido);
break;
default:
System.out.println("\nVocê informou uma opção inválida.\n\n");
}
}
}
|
Mais Desafios de Programação e Exercícios e Algoritmos Resolvidos de Java |
Veja mais Dicas e truques de Java |
Dicas e truques de outras linguagens |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |







