Você está aqui: Cards de Cards de Hidrologia |
||
|
||
|
|
||
R ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cateto oposto dadas as medidas da hipotenusa e do cateto adjascente em RQuantidade de visualizações: 4193 vezes |
|
Todos estamos acostumados com o Teorema de Pitágoras, que diz que "o quadrado da hipotenusa é igual à soma dos quadrados dos catetos". Baseado nessa informação, fica fácil retornar a medida do cateto oposto quando temos as medidas da hipotenusa e do cateto adjascente. Isso, claro, via programação em linguagem R. Comece observando a imagem a seguir:  Veja que, nessa imagem, eu já coloquei os comprimentos da hipotenusa, do cateto oposto e do cateto adjascente. Para facilitar a conferência dos cálculos, eu coloquei também os ângulos theta (que alguns livros chamam de alfa) e beta já devidamente calculados. A medida da hipotenusa é, sem arredondamentos, 36.056 metros. Então, sabendo que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos (Teorema de Pitógoras): \[c^2 = a^2 + b^2\] Tudo que temos que fazer é mudar a fórmula para: \[a^2 = c^2 - b^2\] Veja que agora o quadrado do cateto oposto é igual ao quadrado da hipotenusa menos o quadrado do cateto adjascente. Não se esqueça de que a hipotenusa é o maior lado do triângulo retângulo. Veja agora como esse cálculo é feito em linguagem R (script R):
c <- 36.056 # medida da hipotenusa
b <- 30 # medida do cateto adjascente
# agora vamos calcular o comprimento da cateto oposto
a <- sqrt(c ^ 2 - b ^ 2)
# e mostramos o resultado
paste("A medida do cateto oposto é:", a)
Ao executar este código R nós teremos o seguinte resultado: [1] "A medida do cateto oposto é: 20.0008783807112" Como podemos ver, o resultado retornado com o código R confere com os valores da imagem apresentada. |
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Recursão (Recursividade) |
Exercícios Resolvidos de Java - Como contar de 10 até 0 usando recursividade em Java - Funções recursivas em JavaQuantidade de visualizações: 6834 vezes |
|
Pergunta/Tarefa: Escreva um método recursivo em Java que conta e exibe os valores de 10 até 0. Seu método deverá possuir a seguinte assinatura:
public static void contarRecursivamente(int n){
// sua implementação aqui
}
Sua saída deverá ser parecida com: 10 9 8 7 6 5 4 3 2 1 0 Veja a resolução comentada deste exercício usando Java:
package exercicio;
public class Exercicio {
public static void main(String[] args) {
// efetua uma chamada ao método recursivo
// fornecendo o primeiro valor
contarRecursivamente(10);
}
// método recursivo que conta de 10 até 0;
public static void contarRecursivamente(int n){
// vamos exibir o número atual
System.out.print(n + " ");
// devemos prosseguir com a recursividade?
if(n > 0){
// decrementa o valor de n
n--;
// e faz uma nova chamada recursiva
contarRecursivamente(n);
}
}
}
|
C# ::: Dicas & Truques ::: Recursão (Recursividade) |
Como escrever uma função recursiva para calcular a potência de um número em C# - Curso de C# para iniciantesQuantidade de visualizações: 5047 vezes |
Chamamos de potenciação a operação de se elevar um número (uma base) a um determinado expoente e obter sua potência. Veja a figura a seguir: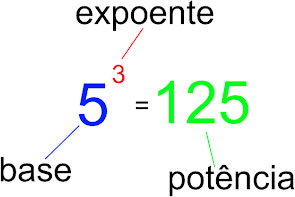 Veja que aqui o valor 5 foi elevado ao cubo, ou seja, ao expoente 3 e obtemos como resultado sua potência: 125. O código abaixo mostra como você pode escrever uma função recursiva em C# que permite calcular a potência de um número inteiro:
using System;
namespace Estudos{
class Program{
// função recursiva que calcula a potência de
// um inteiro
static int potencia(int mbase, int expoente) {
if (expoente == 0) {
return 1;
}
else {
return mbase * potencia(mbase, expoente - 1);
}
}
static void Main(string[] args) {
int mbase = 3; // base
int expoente = 4;
Console.WriteLine(mbase + " elevado a " + expoente +
" = " + potencia(mbase, expoente));
Console.WriteLine("\n\nPressione uma tecla para sair...");
Console.ReadKey();
}
}
}
Ao executar este código C# nós teremos o seguinte resultado: 3 elevado a 4 = 81 |
MySQL ::: Dicas & Truques ::: Data e Hora |
Como usar a função NOW() para obter a data e hora atual do servidor MySQLQuantidade de visualizações: 28515 vezes |
|
As funções CURRENT_TIMESTAMP(), CURRENT_TIMESTAMP, LOCALTIME(), LOCALTIME, LOCALTIMESTAMP e LOCALTIMESTAMP() são sinônimos da função NOW(). A função NOW() pode ser usada para obter a data e hora atual do servidor MySQL como um valor no formato 'YYYY-MM-DD HH:MM:SS' ou YYYYMMDDHHMMSS.uuuuuu, dependendo se a função é usada em um contexto string ou numérico. O valor retornado é expresso no fuso horário atual do servidor. Veja: SELECT NOW() O valor retornado é algo como 2008-03-30 23:18:34. Observe agora uma chamada a esta função em um contexto numérico: SELECT NOW() + 0 O resultado será algo como 20080430232607.000000. |
C# ::: Dicas & Truques ::: Strings e Caracteres |
Como remover espaços em excesso de uma string C# usando expressões regularesQuantidade de visualizações: 15049 vezes |
|
Nesta dica mostrarei como podemos usar expressões regulares em C# para remover os espaços em excesso de uma frase ou texto. Esta técnica é bem útil quando estamos trabalhando com dados informados pelos usuários de nossas aplicações. Temos sempre que verificar, não somente o excesso de espaços no meio do texto, quanto espaços no início e no fim das strings informadas. Veja o código completo para o exemplo:
using System;
using System.Text.RegularExpressions;
namespace Estudos {
class Program {
static void Main(string[] args) {
// vamos construir o Regex com o padrão que queremos
Regex regex = new Regex("\\s +", RegexOptions.IgnoreCase |
RegexOptions.Compiled);
// frase com espaços
string frase = " Gosto muito de C# ";
// frase sem espaços
string resultado = (regex.Replace(frase, " ")).Trim();
// mostramos o resultado
Console.WriteLine("Frase com espaços em excesso: {0}", frase);
Console.WriteLine("Espaços em excesso removidos: {0}", resultado);
Console.WriteLine("\n\nPressione uma tecla para sair...");
Console.ReadKey();
}
}
}
Ao executar este código C# nós teremos o seguinte resultado:
Frase com espaços em excesso:
Gosto muito de C#
Espaços em excesso removidos:
Gosto muito de C#
|
Desafios, Exercícios e Algoritmos Resolvidos de C# |
Veja mais Dicas e truques de C# |
Dicas e truques de outras linguagens |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |






