Você está aqui: Cards de Engenharia Civil - Estruturas de Aço e Madeira |
||
|
||
|
|
||
LISP ::: Fundamentos da Linguagem ::: Estruturas de Controle |
Como usar o laço loop para contar de 1 até 10 em LispQuantidade de visualizações: 661 vezes |
|
A estrutura de repetição loop da linguagem Common Lisp é o laço mais simples fornecido pela linguagem. Este laço nos permite repetir uma ou mais instruções de código repetidamente, até que o comando return seja encontrado, o que faz com que o laço seja interrompido. Veja no trecho de código abaixo como podemos usar o laço loop da Common Lisp para contar e exibir os valores de 1 até 10:
(
; vamos declarar a variável que vamos usar
let (numero)
; vamos inicializar a variável com o valor 1
(setq numero 1)
; agora iniciamos o laço
(loop
; escrevemos o valor da variável
(write numero)
; aumentamos o valor da variável em 1
(setq numero (+ numero 1))
; provocamos uma quebra de linha
(terpri)
; e fazemos o teste da continuidade
(when (> numero 10) (return))
)
)
Ao executarmos este código Common Lisp nós teremos o seguinte resultado: 1 2 3 4 5 6 7 8 9 10 Veja que usamos a macro when para testar o ponto de parada do laço. Note ainda o uso da função terpri da Common Lisp para provocar uma quebra de linha na saída do programa. |
Delphi ::: Dicas & Truques ::: Matemática e Estatística |
Como calcular desvio padrão em Delphi - Delphi para Matemática e EstatísticaQuantidade de visualizações: 2117 vezes |
|
Em Matemática e Estatística, o Desvio padrão (em inglês: Standard Deviation) é uma medida de dispersão, ou seja, é uma medida que indica o quanto um conjunto de dados é uniforme. Quando o desvio padrão é baixo, isso quer dizer que os dados do conjunto estão mais próximos da média. Como calcular o desvio padrão de um conjunto de dados? Vamos começar analisando a fórmula mais difundida na matemática e na estatística: \[\sigma = \sqrt{ \frac{\sum_{i=1}^N (x_i -\mu)^2}{N}}\] Onde: a) __$\sigma__$ é o desvio; b) __$x_i__$ é um valor qualquer no conjunto de dados na posição i; c) __$\mu__$ é a média aritmética dos valores do conjunto de dados; d) N é a quantidade de valores no conjunto. O somatório dentro da raiz quadrada nos diz que devemos somar todos os elementos do conjunto, desde a posição 1 até a posição n, subtrair cada valor pela média do conjunto e elevar ao quadrado. Obtida a soma, nós a dividimos pelo tamanho do conjunto. Veja o código Delphi completo que obtém o desvio padrão a partir de um conjunto de dados contendo quatro valores:
// Algoritmo Delphi para calcular desvio padrão
program estudos_delphi;
{$APPTYPE CONSOLE}
uses
SysUtils, Math;
var
// conjunto de dados
conjunto: array[1..4] of double = (10, 30, 90, 30);
soma: double; // Soma dos elementos
desvio_padrao: double; // Desvio padrão
tam: integer; // Tamanho dos dados
media: double; // média
i: integer;
begin
soma := 0.0;
desvio_padrao := 0.0;
tam := 4;
// vamos somar todos os elementos
for i := 1 to tam do
begin
soma := soma + conjunto[i];
end;
// agora obtemos a média do conjunto de dados
media := soma / tam;
// e finalmente obtemos o desvio padrão
for i := 1 to tam do
begin
// não esqueça de adicionar a unit Math
desvio_padrao := desvio_padrao + Power(conjunto[i] - media, 2);
end;
// mostramos o resultado
WriteLn('Desvio Padrão Populacional: ' + FloatToStr(Sqrt(desvio_padrao / tam)));
WriteLn('Desvio Padrão Amostral: ' + FloatToStr(Sqrt(desvio_padrao / (tam - 1))));
WriteLn;
Write('Pressione Enter para sair...');
ReadLn;
end.
Ao executar este código Delphi nós teremos o seguinte resultado: Desvio Padrão Populacional: 30.0 Desvio Padrão Amostral: 34.64101615137755 Veja que, para calcular o Desvio Padrão Populacional, nós dividimos o somatório pela quantidade de elementos no conjunto, enquanto, para calcular o Desvio Padrão Amostral, nós dividimos o somatório pela quantidade de elementos - 1 (cuidado com a divisão por zero no caso de um conjunto com apenas um elemento). |
Dart ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cosseno de um ângulo em Dart usando o método cos() da biblioteca Math - Calculadora de cosseno em DartQuantidade de visualizações: 827 vezes |
|
Em geral, quando falamos de cosseno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função cosseno disponível nas linguagens de programação para calcular o cosseno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função cosseno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o cosseno é a razão entre o cateto adjascente e a hipotenusa, ou seja, o cateto adjascente dividido pela hipotenusa. Veja a fórmula: \[\text{Cosseno} = \frac{\text{Cateto adjascente}}{\text{Hipotenusa}} \] Então, se dividirmos 30 por 36.056 (na figura eu arredondei) nós teremos 0.8320, que é a razão entre o cateto adjascente e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.8320. O resultado será 0.5881 (em radianos). Convertendo 0.5881 radianos para graus, nós obtemos 33.69º, que é exatamente o ângulo em graus entre o cateto adjascente e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é cosseno na trigonometria, vamos entender mais sobre a função cos() da linguagem Dart. Esta método, que faz parte da biblioteca Math, recebe um valor numérico e retorna um valor, também numérico) entre -1 até 1 (ambos inclusos). Veja:
// vamos importar a biblioteca dart:math
import "dart:math";
void main(){
print("Cosseno de 0 = " + cos(0).toString());
print("Cosseno de 1 = " + cos(1).toString());
print("Cosseno de 2 = " + cos(2).toString());
}
Ao executar este código Dart nós teremos o seguinte resultado: Cosseno de 0 = 1.0 Cosseno de 1 = 0.5403023058681398 Cosseno de 2 = -0.4161468365471424 Note que calculamos os cossenos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função cosseno mostrada abaixo: 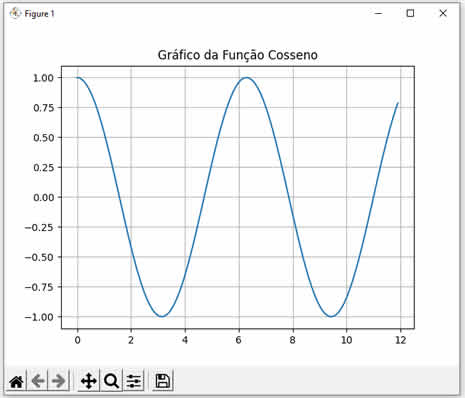 |
PHP ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular a equação reduzida da reta em PHP dados dois pontos pertencentes à retaQuantidade de visualizações: 917 vezes |
|
Nesta dica de PHP veremos como calcular a equação reduzida da reta quando temos dois pontos pertencentes à esta reta. Não, nessa dica não vamos calcular a equação geral da reta, apenas a equação reduzida. Em outras dicas do site você encontra como como isso pode ser feito. Para relembrar: a equação reduzida da reta é y = mx + n, em que x e y são, respectivamente, a variável independente e a variável dependente; m é o coeficiente angular, e n é o coeficiente linear. Além disso, m e n são números reais. Com a equação reduzida da reta, é possível calcular quais são os pontos que pertencem a essa reta e quais não pertencem. Vamos começar então analisando a seguinte figura, na qual temos dois pontos que pertencem à uma reta: 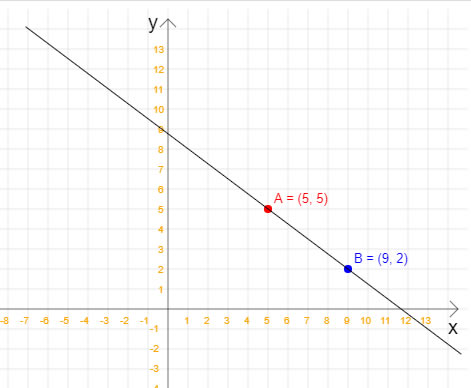 Note que a reta da figura passa pelos pontos A(5, 5) e B(9, 2). Então, uma vez que já temos os dois pontos, já podemos calcular a equação reduzida da reta. Veja o código PHP completo para esta tarefa:
<?php
// para executar abra uma janela de comando
// cmd e dispare o comando abaixo:
// C:\xampp\php>php c:\estudos_php\estudos.php
// para ler a entrada do usuário
$entrada = fopen("php://stdin","r");
// vamos ler as coordenadas do primeiro ponto
echo "Coordenada x do primeiro ponto: ";
$x1 = fgets($entrada);
echo "Coordenada y do primeiro ponto: ";
$y1 = fgets($entrada);
// vamos ler as coordenadas do segundo ponto
echo "Coordenada x do segundo ponto: ";
$x2 = fgets($entrada);
echo "Coordenada y do segundo ponto: ";
$y2 = fgets($entrada);
$sinal = "+";
// vamos calcular o coeficiente angular da reta
$m = ($y2 - $y1) / ($x2 - $x1);
// vamos calcular o coeficiente linear
$n = $y1 - ($m * $x1);
// coeficiente linear menor que zero? O sinal será negativo
if ($n < 0){
$sinal = "-";
$n = $n * -1;
}
// mostra a equação reduzida da reta
echo "Equação reduzida: y = " . $m . "x"
. " " . $sinal . " " . $n;
?>
Ao executar este código PHP nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 5 Coordenada y do primeiro ponto: 5 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 2 Equação reduzida: y = -0,75x + 8,75 Para testarmos se nossa equação reduzida da reta está realmente correta, considere o valor 3 para o eixo x da imagem acima. Ao efetuarmos o cálculo: >> y = (-0.75 * 3) + 8.75 y = 6.5000 temos o valor 6.5 para o eixo y, o que faz com que o novo ponto caia exatamente em cima da reta considerada na imagem. |
Java ::: Classes e Componentes ::: JTextArea |
Java Swing - Como obter o texto selecionado em um controle JTextArea do Java SwingQuantidade de visualizações: 19 vezes |
|
Em algumas situações nós precisamos obter o texto selecionado pelo usuário em um componente JTextArea de nossas aplicações Java Swing. Isso pode ser feito com uma chamada ao seu método getSelectedText(). Veja um trecho de código no qual obtemos o texto selecionado em um JTextArea chamado textArea: textArea = new JTextArea(10, 20); String selecionado = textArea.getSelectedText(); |
Desafios, Exercícios e Algoritmos Resolvidos de Java |
Veja mais Dicas e truques de Java |
Dicas e truques de outras linguagens |
|
JavaScript - Como ordenar um array de strings em ordem alfabética em JavaScript - Vetores e matrizes em JavaScript |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |






